题目内容
已知函数f(x)=2x2+3(a2+a)lnx-8ax.
(Ⅰ)若曲线f(x)在点(1,f(1))处的切线与直线y=32x-62平行,求a的值;
(Ⅱ)若函数f(x)在其导函数f′(x)的单调区间上也是单调的,求a的取值范围.
(Ⅰ)若曲线f(x)在点(1,f(1))处的切线与直线y=32x-62平行,求a的值;
(Ⅱ)若函数f(x)在其导函数f′(x)的单调区间上也是单调的,求a的取值范围.
考点:利用导数研究函数的单调性,利用导数研究曲线上某点切线方程
专题:导数的综合应用
分析:(Ⅰ)对函数f(x)=2x2+3(a2+a)lnx-8ax求导.因为曲线y=f(x)在点(1,f(1))处的切线与直线y=32x-62平行,则切线的斜率k=32.由此能求出实数a;
(Ⅱ)求导函数f′(x)=
(x>0),构造新函数g(x)=4x2-8ax+3(a2+a),设g(x)=0的两根x1,x2(x1<x2),分类讨论,通过比较根的关系,根据f(x)在f′(x)的单调区间上也是单调的,即可确定实数a的范围.
(Ⅱ)求导函数f′(x)=
| 4x2-8ax+3(a2+a) |
| x |
解答:
解:(Ⅰ)由于函数f(x)=2x2+3(a2+a)lnx-8ax,则f′(x)=4x+3(a2+a)•
-8a.
因为曲线y=f(x)在点(1,f(1))处的切线与直线y=32x-62平行,
则切线的斜率k=32,即3a2-5a-28=0,解得或a=-
.
而当a=-
时,切线与y=32x-62平行,符合题意
当a=4时,切线为y=32x-62重合,不合条件,舍去
故a=-
.
(Ⅱ)f′(x)=4x+3(a2+a)•
-8a=
,
设g(x)=4x2-8ax+3(a2+a),△=16(a2-3a),
设g(x)=0的两根为x1,x2(x1<x2)
(1)当△≤0即0≤a≤3时,f′(x)≥0,∴f(x)单调递增,满足题意;
(2)当△>0即a<0或a>3时,
①若x1<0<x2,则
(a2+a)<0,即-1<a<0,
此时,f(x)在(0,x2)上单调递减,在(x2,+∞)上单调递增,
而f′(x)在(0,+∞)上单调递增,故不满足题意
②若x1<x2≤0,则
解得a≤-1,
此时,f(x)在(0,+∞)上单调递增,满足题意
③若0<x1<x2,则
解得a>0,
此时,f(x)在(0,x1 )上单调递增,(x1,x2)上单调递减,在(x2,+∞)上单调递增,故不满足题意
综上得a的取值范围为(-∞,-1]∪[0,3].
| 1 |
| x |
因为曲线y=f(x)在点(1,f(1))处的切线与直线y=32x-62平行,
则切线的斜率k=32,即3a2-5a-28=0,解得或a=-
| 7 |
| 3 |
而当a=-
| 7 |
| 3 |
当a=4时,切线为y=32x-62重合,不合条件,舍去
故a=-
| 7 |
| 3 |
(Ⅱ)f′(x)=4x+3(a2+a)•
| 1 |
| x |
| 4x2-8ax+3(a2+a) |
| x |
设g(x)=4x2-8ax+3(a2+a),△=16(a2-3a),
设g(x)=0的两根为x1,x2(x1<x2)
(1)当△≤0即0≤a≤3时,f′(x)≥0,∴f(x)单调递增,满足题意;
(2)当△>0即a<0或a>3时,
①若x1<0<x2,则
| 3 |
| 4 |
此时,f(x)在(0,x2)上单调递减,在(x2,+∞)上单调递增,
而f′(x)在(0,+∞)上单调递增,故不满足题意
②若x1<x2≤0,则
|
此时,f(x)在(0,+∞)上单调递增,满足题意
③若0<x1<x2,则
|
此时,f(x)在(0,x1 )上单调递增,(x1,x2)上单调递减,在(x2,+∞)上单调递增,故不满足题意
综上得a的取值范围为(-∞,-1]∪[0,3].
点评:本题考查导数知识的运用,考查函数的单调性与极值,考查分类讨论的数学思想,正确分类是关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
复数z=
(其中i为虚数单位)在复平面内对应的点在( )
| 1+3i |
| i |
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
设复数z=1-2i(i为虚数单位),则复数z的虚部为( )
| A、-2 | B、2 | C、-2i | D、2i |
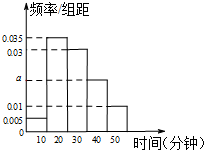 某学校为调查高一新生上学路程所需要的时间(单位:分钟),从高一年级新生中随机抽取100名新生按上学所需时间分组:第1组(0,10],第2组(10,20],第3组(20,30],第4组(30,40],第5组(40,50],得到的频率分布直方图如图所示.
某学校为调查高一新生上学路程所需要的时间(单位:分钟),从高一年级新生中随机抽取100名新生按上学所需时间分组:第1组(0,10],第2组(10,20],第3组(20,30],第4组(30,40],第5组(40,50],得到的频率分布直方图如图所示.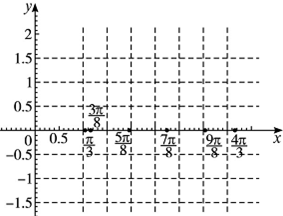 已知函数f(x)=
已知函数f(x)=