题目内容
9.直线l:x+4y=2与圆C:x2+y2=1交于A、B两点,O为坐标原点,若直线OA、OB的倾斜角分别为α、β,则cosα+cosβ=( )| A. | $\frac{18}{17}$ | B. | $-\frac{12}{17}$ | C. | $-\frac{4}{17}$ | D. | $\frac{4}{17}$ |
分析 设A(x1,y1),B(x2,y2),由三角函数的定义得:cosα+cosβ=x1+x2,由此利用韦达定理能求出cosα+cosβ的值.
解答 解:设A(x1,y1),B(x2,y2),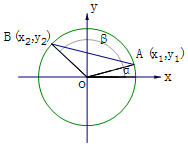
由三角函数的定义得:cosα+cosβ=x1+x2,
由$\left\{\begin{array}{l}x+4y=2\\{x^2}+{y^2}=1.\end{array}\right.$,消去y得:17x2-4x-12=0
则${x_1}+{x_2}=\frac{4}{17}$,
即$cosα+cosβ=\frac{4}{17}$.
故选:D.
点评 本题考查两个角的余弦值之和的求法,是基础题,解题时要认真审题,注意韦达定理和三角函数定义的合理运用.

练习册系列答案
相关题目
19.双曲线$\frac{x^2}{4}-\frac{y^2}{12}=1$的焦点到渐近线的距离为( )
| A. | $2\sqrt{3}$ | B. | 2 | C. | $\sqrt{3}$ | D. | 1 |
20.若a>0,且a≠1,则“函数y=ax在R上是减函数”是“函数y=(2-a)x3在R上是增函数”的( )
| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
4.设D为△ABC所在平面内一点,且$\overrightarrow{BC}=3\overrightarrow{BD}$,则$\overrightarrow{AD}$=( )
| A. | $\frac{2}{3}\overrightarrow{AB}+\frac{1}{3}\overrightarrow{AC}$ | B. | $\frac{1}{3}\overrightarrow{AB}+\frac{2}{3}\overrightarrow{AC}$ | C. | $\frac{4}{3}\overrightarrow{AB}+\frac{1}{3}\overrightarrow{AC}$ | D. | $\frac{2}{3}\overrightarrow{AB}+\frac{5}{3}\overrightarrow{AC}$ |
1.阅读如图所示的程序框图,运行相应程序,输出的结果是( )


| A. | 242 | B. | 274 | C. | 275 | D. | 338 |
18.已知全集U=R,集合A={x|x2>1},那么∁UA=( )
| A. | [-1,1] | B. | [1,+∞) | C. | (-∞,1] | D. | (-∞,-1]∪[1,+∞) |
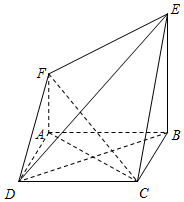 如图,四边形ABCD是边长为2的正方形,平面ABCD⊥平面ABEF,AF∥BE,AB⊥BE,AB=BE=2,AF=1.
如图,四边形ABCD是边长为2的正方形,平面ABCD⊥平面ABEF,AF∥BE,AB⊥BE,AB=BE=2,AF=1.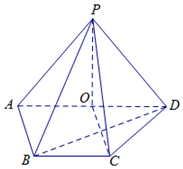 如图,在四棱锥P-ABCD中,O∈AD,AD∥BC,AB⊥AD,AO=AB=BC=1,PO=$\sqrt{2}$,$PC=\sqrt{3}$.
如图,在四棱锥P-ABCD中,O∈AD,AD∥BC,AB⊥AD,AO=AB=BC=1,PO=$\sqrt{2}$,$PC=\sqrt{3}$.