题目内容
19.双曲线$\frac{x^2}{4}-\frac{y^2}{12}=1$的焦点到渐近线的距离为( )| A. | $2\sqrt{3}$ | B. | 2 | C. | $\sqrt{3}$ | D. | 1 |
分析 先由题中条件求出焦点坐标和渐近线方程,再代入点到直线的距离公式即可求出结论.
解答 解:由题得:其焦点坐标为(-4,0),(4,0),渐近线方程为y=±$\sqrt{3}$x
所以焦点到其渐近线的距离d=$\frac{4\sqrt{3}}{\sqrt{1+3}}$=2$\sqrt{3}$.
故选:A
点评 本题考查双曲线的标准方程,以及双曲线的简单性质,点到直线的距离公式的应用,属于基础题.

练习册系列答案
相关题目
10.平面向量$\overrightarrow{a}$=(x,1),$\overrightarrow{b}$=(1,y),$\overrightarrow{c}$=(2,-4),如果 $\overrightarrow{b}$∥$\overrightarrow{c}$,且$\overrightarrow{a}$⊥($\overrightarrow{b}$-$\overrightarrow{c}$),那么实数x,y的值分别是( )
| A. | 2,-2 | B. | -2,-2 | C. | $\frac{1}{2}$,2 | D. | $\frac{1}{2}$,$\frac{1}{2}$ |
7.已知函数f(x)的定义域为R,且为可导函数,若对?x∈R,总有2f(x)+xf′(x)<0成立(其中f′(x)是f(x)的导函数),则( )
| A. | f(x)>0恒成立 | B. | f(x)<0恒成立 | ||
| C. | f(x)的最大值为0 | D. | f(x)与0的大小关系不确定 |
4.已知$\overrightarrow{AB}$=(1,1),$\overrightarrow{BC}$=(x,-3),若$\overrightarrow{AC}$⊥$\overrightarrow{AB}$,则x=( )
| A. | 3 | B. | 1 | C. | -3或2 | D. | -4或1 |
11.已知函数f(x)=Asin(ωx+φ)(ω>0,-π<φ<0)的部分图象如图所示,则下列判断正确的是( )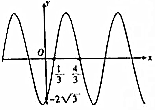

| A. | 函数f(x)的最小正周期为π | |
| B. | 函数f(x)的值域为[-$\frac{7}{2}$,$\frac{7}{2}$] | |
| C. | 函数f(x)的图象关于直线x=-$\frac{1}{6}$对称 | |
| D. | 函数f(x)的图象向右平移$\frac{1}{3}$个单位得到函数y=Asinωx的图象 |
9.直线l:x+4y=2与圆C:x2+y2=1交于A、B两点,O为坐标原点,若直线OA、OB的倾斜角分别为α、β,则cosα+cosβ=( )
| A. | $\frac{18}{17}$ | B. | $-\frac{12}{17}$ | C. | $-\frac{4}{17}$ | D. | $\frac{4}{17}$ |