题目内容
4.设D为△ABC所在平面内一点,且$\overrightarrow{BC}=3\overrightarrow{BD}$,则$\overrightarrow{AD}$=( )| A. | $\frac{2}{3}\overrightarrow{AB}+\frac{1}{3}\overrightarrow{AC}$ | B. | $\frac{1}{3}\overrightarrow{AB}+\frac{2}{3}\overrightarrow{AC}$ | C. | $\frac{4}{3}\overrightarrow{AB}+\frac{1}{3}\overrightarrow{AC}$ | D. | $\frac{2}{3}\overrightarrow{AB}+\frac{5}{3}\overrightarrow{AC}$ |
分析 根据向量的三角形法则进行转化求解即可.
解答  解:∵$\overrightarrow{BC}=3\overrightarrow{BD}$
解:∵$\overrightarrow{BC}=3\overrightarrow{BD}$
∴$\overrightarrow{BD}$=$\frac{1}{3}$$\overrightarrow{BC}$=$\frac{1}{3}$($\overrightarrow{AC}$-$\overrightarrow{AB}$),
则$\overrightarrow{AD}$=$\overrightarrow{AB}$+$\overrightarrow{BD}$=$\overrightarrow{AB}$+$\frac{1}{3}$($\overrightarrow{AC}$-$\overrightarrow{AB}$)=$\frac{2}{3}\overrightarrow{AB}+\frac{1}{3}\overrightarrow{AC}$,
故选:A
点评 本题主要考查向量的分解,根据向量三角形法则进行转化是解决本题的关键.

练习册系列答案
相关题目
12.复数$\frac{2}{1+i}$=( )
| A. | 2-i | B. | 2-2i | C. | 1+i | D. | 1-i |
9.直线l:x+4y=2与圆C:x2+y2=1交于A、B两点,O为坐标原点,若直线OA、OB的倾斜角分别为α、β,则cosα+cosβ=( )
| A. | $\frac{18}{17}$ | B. | $-\frac{12}{17}$ | C. | $-\frac{4}{17}$ | D. | $\frac{4}{17}$ |
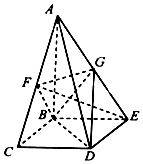 如图所示,在四棱锥A-BCDE中,AB⊥平面BCDE,四边形BCDE为矩形,F、G分别为AC、AE的中点,AB=BC=2,BE=$\sqrt{2}$.
如图所示,在四棱锥A-BCDE中,AB⊥平面BCDE,四边形BCDE为矩形,F、G分别为AC、AE的中点,AB=BC=2,BE=$\sqrt{2}$.