题目内容
14.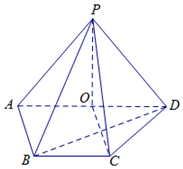 如图,在四棱锥P-ABCD中,O∈AD,AD∥BC,AB⊥AD,AO=AB=BC=1,PO=$\sqrt{2}$,$PC=\sqrt{3}$.
如图,在四棱锥P-ABCD中,O∈AD,AD∥BC,AB⊥AD,AO=AB=BC=1,PO=$\sqrt{2}$,$PC=\sqrt{3}$.(Ⅰ)证明:平面POC⊥平面PAD;
(Ⅱ)若AD=2,PA=PD,求CD与平面PAB所成角的余弦值.
分析 (Ⅰ)证明:OC⊥平面PAD,即可证明平面POC⊥平面PAD;
(Ⅱ)若AD=2,PA=PD,点O作OE⊥PA于E,连结BE,则OE⊥平面PAB,∠OBE为CD与平面PAB所成的角,即可求CD与平面PAB所成角的余弦值.
解答  (Ⅰ)证明:在四边形OABC中,
(Ⅰ)证明:在四边形OABC中,
∵AO∥BC,AO=BC,AB⊥AD,
∴四边形OABC是正方形,得OC⊥AD,-----------------------(2分)
在△POC中,∵PO2+OC2=PC2,∴OC⊥PO,-------(4分)
又PO∩AD=O,∴OC⊥平面PAD,
又OC?平面POC,∴平面POC⊥平面PAD;-------------(6分)
(Ⅱ)解:连结OB,
∵OD∥BC,且OD=BC∴BCDO为平行四边形,∴OB∥CD,----------------------------(7分)
由(Ⅰ)知OC⊥平面PAD,∴AB⊥平面PAD,
∵AB?平面PAB,∴平面PAB⊥平面PAD,----------------------------------------------------(8分)
过点O作OE⊥PA于E,连结BE,则OE⊥平面PAB,
∴∠OBE为CD与平面PAB所成的角,----------------------(10分)
在Rt△OEB中,∵$OE=\frac{PO•AO}{PA}=\frac{{\sqrt{2}}}{{\sqrt{3}}}$,$OB=\sqrt{2}$,
∴$cos∠OBE=\frac{BE}{OB}=\frac{{\sqrt{2-\frac{6}{9}}}}{{\sqrt{2}}}=\frac{{\sqrt{6}}}{3}$,
即CD与平面PAB所成角的余弦值为$\frac{{\sqrt{6}}}{3}$.--------------------------------------------------(12分)
点评 本题考查线面、面垂直的证明,考查线面角,考查学生分析解决问题的能力,属于中档题.

| A. | 3 | B. | 1 | C. | -3或2 | D. | -4或1 |
| A. | $\frac{18}{17}$ | B. | $-\frac{12}{17}$ | C. | $-\frac{4}{17}$ | D. | $\frac{4}{17}$ |
| A. | $\sqrt{5}$ | B. | $\frac{{\sqrt{5}}}{2}$ | C. | 2 | D. | $\sqrt{2}$ |
| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
$\frac{周实际回收水费}{周投入成本}$”表示每周“水站诚信度”.为了便于数据分析,以四周为一个周期,下表为该水站连续八周(共两个周期)的诚信度数据统计,如表1:
| 第一周 | 第二周 | 第三周 | 第四周 | |
| 第一个周期 | 95% | 98% | 92% | 88% |
| 第二个周期 | 94% | 94% | 83% | 80% |
(Ⅱ)从表1诚信度超过91% 的数据中,随机抽取2个,求至少有1个数据出现在第二个周期的概率;
(Ⅲ)学生会认为水站诚信度在第二个周期中的后两周出现了滑落,为此学生会举行了“以诚信为本”主题教育活动,并得到活动之后一个周期的水站诚信度数据,如表2:
| 第一周 | 第二周 | 第三周 | 第四周 | |
| 第三个周期 | 85% | 92% | 95% | 96% |
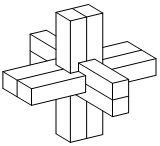 鲁班锁是中国传统的智力玩具,起源于古代汉族建筑中首创的榫卯结构,这种三维的拼插器具内部的凹凸部分(即榫卯结构)啮合,十分巧妙,外观看是严丝合缝的十字立方体,其上下、左右、前后完全对称.从外表上看,六根等长的正四棱柱体分成三组,经90°榫卯起来,如图3,若正四棱柱体的高为6,底面正方形的边长为1,现将该鲁班锁放进一个球形容器内,则该球形容器的表面积的最小值为41π.(容器壁的厚度忽略不计)
鲁班锁是中国传统的智力玩具,起源于古代汉族建筑中首创的榫卯结构,这种三维的拼插器具内部的凹凸部分(即榫卯结构)啮合,十分巧妙,外观看是严丝合缝的十字立方体,其上下、左右、前后完全对称.从外表上看,六根等长的正四棱柱体分成三组,经90°榫卯起来,如图3,若正四棱柱体的高为6,底面正方形的边长为1,现将该鲁班锁放进一个球形容器内,则该球形容器的表面积的最小值为41π.(容器壁的厚度忽略不计)