题目内容
17.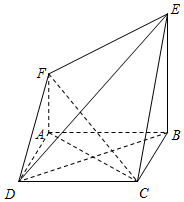 如图,四边形ABCD是边长为2的正方形,平面ABCD⊥平面ABEF,AF∥BE,AB⊥BE,AB=BE=2,AF=1.
如图,四边形ABCD是边长为2的正方形,平面ABCD⊥平面ABEF,AF∥BE,AB⊥BE,AB=BE=2,AF=1.(Ⅰ)求证:AC⊥平面BDE;
(Ⅱ)求证:AC∥平面DEF;
(Ⅲ)求三棱锥C-DEF的体积.
分析 (Ⅰ)推导出BE⊥AC,AC⊥BD.由此能证明AC⊥平面BDE.
(Ⅱ)设AC∩BD=O,设G为DE的中点,连结OG,FG,推导出四边形AOGF为平行四边形,从而AO∥FG,即AC∥FG,由此能证明AC∥平面DEF.
(Ⅲ)推导出点C到平面DEF的距离等于A点到平面DEF的距离,由VC-DEF=VA-DEF,能求出三棱锥C-DEF的体积.
解答 (本小题满分14分)
证明:(Ⅰ)因为平面ABCD⊥平面ABEF,
平面ABCD∩平面ABEF=AB,且AB⊥BE,所以BE⊥平面ABCD.
因为AC?平面ABCD,所以BE⊥AC.
又因为四边形ABCD为正方形,所以AC⊥BD.
因为BD∩BE=B,所以AC⊥平面BDE.…(4分)
(Ⅱ)设AC∩BD=O,
因为四边形ABCD为正方形,所以O为BD中点.
设G为DE的中点,连结OG,FG,
则OG∥BE,且$OG=\frac{1}{2}BE$.由已知AF∥BE,且$AF=\frac{1}{2}BE$,
则AF∥OG,且AF=OG.所以四边形AOGF为平行四边形.
所以AO∥FG,即AC∥FG.
因为AC?平面DEF,FG?平面DEF,
所以AC∥平面DEF.…(9分)
解:(Ⅲ)由(Ⅰ)可知BE⊥平面ABCD,
因为AF∥BE,所以AF⊥平面ABCD,所以AF⊥AB,AF⊥AD.
又因为四边形ABCD为正方形,所以AB⊥AD,
所以AD⊥平面ABEF.
由(Ⅱ)可知,AC∥平面DEF,
所以,点C到平面DEF的距离等于A点到平面DEF的距离,
所以 VC-DEF=VA-DEF.
因为AB=AD=2AF=2.
所以${V_{C-DEF}}={V_{A-DEF}}={V_{D-AEF}}=\frac{1}{3}×{S_{△AEF}}×AD=\frac{1}{3}×\frac{1}{2}×AF×AB×AD$=$\frac{1}{3}×\frac{1}{2}×1×2×2=\frac{2}{3}$.
故三棱锥C-DEF的体积为$\frac{2}{3}$.…(14分)
点评 本题考查线面垂直的证明,考查线面平行的证明,考查三棱锥的体积的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.

 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案| A. | f(x)>0恒成立 | B. | f(x)<0恒成立 | ||
| C. | f(x)的最大值为0 | D. | f(x)与0的大小关系不确定 |
| A. | 2-i | B. | 2-2i | C. | 1+i | D. | 1-i |
| A. | $\frac{18}{17}$ | B. | $-\frac{12}{17}$ | C. | $-\frac{4}{17}$ | D. | $\frac{4}{17}$ |
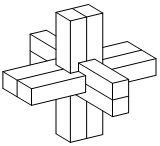 鲁班锁是中国传统的智力玩具,起源于古代汉族建筑中首创的榫卯结构,这种三维的拼插器具内部的凹凸部分(即榫卯结构)啮合,十分巧妙,外观看是严丝合缝的十字立方体,其上下、左右、前后完全对称.从外表上看,六根等长的正四棱柱体分成三组,经90°榫卯起来,如图3,若正四棱柱体的高为6,底面正方形的边长为1,现将该鲁班锁放进一个球形容器内,则该球形容器的表面积的最小值为41π.(容器壁的厚度忽略不计)
鲁班锁是中国传统的智力玩具,起源于古代汉族建筑中首创的榫卯结构,这种三维的拼插器具内部的凹凸部分(即榫卯结构)啮合,十分巧妙,外观看是严丝合缝的十字立方体,其上下、左右、前后完全对称.从外表上看,六根等长的正四棱柱体分成三组,经90°榫卯起来,如图3,若正四棱柱体的高为6,底面正方形的边长为1,现将该鲁班锁放进一个球形容器内,则该球形容器的表面积的最小值为41π.(容器壁的厚度忽略不计)