题目内容
20.若a>0,且a≠1,则“函数y=ax在R上是减函数”是“函数y=(2-a)x3在R上是增函数”的( )| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
分析 根据函数单调性之间的关系以及充分条件和必要条件的定义进行判断即可.
解答 解:若函数y=ax在R上是减函数,则0<a<1,此时2-a>0,则函数y=(2-a)x3在R上是增函数成立,即充分性成立,
若函数y=(2-a)x3在R上是增函数,则2-a>0,即0<a<2,则函数y=ax在R上不一定是减函数,即必要性不成立,
即“函数y=ax在R上是减函数”是“函数y=(2-a)x3在R上是增函数”的充分不必要条件,
故选:A.
点评 本题主要考查充分条件和必要条件的判断,根据函数单调性的性质是解决本题的关键.

练习册系列答案
相关题目
10.平面向量$\overrightarrow{a}$=(x,1),$\overrightarrow{b}$=(1,y),$\overrightarrow{c}$=(2,-4),如果 $\overrightarrow{b}$∥$\overrightarrow{c}$,且$\overrightarrow{a}$⊥($\overrightarrow{b}$-$\overrightarrow{c}$),那么实数x,y的值分别是( )
| A. | 2,-2 | B. | -2,-2 | C. | $\frac{1}{2}$,2 | D. | $\frac{1}{2}$,$\frac{1}{2}$ |
11.已知函数f(x)=Asin(ωx+φ)(ω>0,-π<φ<0)的部分图象如图所示,则下列判断正确的是( )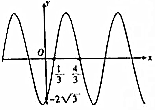

| A. | 函数f(x)的最小正周期为π | |
| B. | 函数f(x)的值域为[-$\frac{7}{2}$,$\frac{7}{2}$] | |
| C. | 函数f(x)的图象关于直线x=-$\frac{1}{6}$对称 | |
| D. | 函数f(x)的图象向右平移$\frac{1}{3}$个单位得到函数y=Asinωx的图象 |
12.复数$\frac{2}{1+i}$=( )
| A. | 2-i | B. | 2-2i | C. | 1+i | D. | 1-i |
9.直线l:x+4y=2与圆C:x2+y2=1交于A、B两点,O为坐标原点,若直线OA、OB的倾斜角分别为α、β,则cosα+cosβ=( )
| A. | $\frac{18}{17}$ | B. | $-\frac{12}{17}$ | C. | $-\frac{4}{17}$ | D. | $\frac{4}{17}$ |
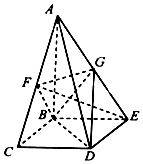 如图所示,在四棱锥A-BCDE中,AB⊥平面BCDE,四边形BCDE为矩形,F、G分别为AC、AE的中点,AB=BC=2,BE=$\sqrt{2}$.
如图所示,在四棱锥A-BCDE中,AB⊥平面BCDE,四边形BCDE为矩形,F、G分别为AC、AE的中点,AB=BC=2,BE=$\sqrt{2}$. A、B两个班共有65名学生,为调查他们的引体向上锻炼情况,通过分层抽样获得了部分学生引体向上的测试数据(单位:个),用茎叶图记录如下:
A、B两个班共有65名学生,为调查他们的引体向上锻炼情况,通过分层抽样获得了部分学生引体向上的测试数据(单位:个),用茎叶图记录如下: