题目内容
16.已知$tan({π-α})=\frac{3}{4},α∈({\frac{π}{2},π})$,则cosα=( )| A. | $-\frac{4}{5}$ | B. | $\frac{4}{5}$ | C. | $-\frac{3}{5}$ | D. | $\frac{3}{5}$ |
分析 利用诱导公式化解可得tanα的值,利用同角三角函数关系式可得答案.
解答 解:由$tan({π-α})=\frac{3}{4},α∈({\frac{π}{2},π})$,
则tanα=$-\frac{3}{4}$,即$\frac{sinα}{cosα}=-\frac{3}{4}$…①
又sin2α+cos2α=1…②,
由①②解得:cosα=$-\frac{4}{5}$.
故选A.
点评 本题考查了诱导公式化解和同角三角函数关系式的计算能力,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
7.某几何体的三视图如图所示,则该几何体的体积等于( )


| A. | 6+6π | B. | 6+8π | C. | 8+6π | D. | 8+8π |
11.(1+$\sqrt{x}}$)6(1+$\sqrt{x}$)4的展开式中x的系数是( )
| A. | -4 | B. | 21 | C. | 45 | D. | 4 |
1.已知函数$f(x)=\left\{\begin{array}{l}-2x-{x^2},x≤0\\|{lgx}|,x>0\end{array}\right.$,若a<b<c<d,且f(a)=f(b)=f(c)=f(d),则a+b+c+2d的取值范围是( )
| A. | $({3,\frac{201}{10}})$ | B. | $({1,\frac{181}{10}})$ | C. | $({2\sqrt{2},+∞})$ | D. | $({2\sqrt{2}-2,+∞})$ |
5.若$A({3,\frac{π}{3}})$,$B({3,\frac{7π}{6}})$,则△AOB的面积为( )
| A. | $\frac{{\sqrt{3}}}{4}$ | B. | 3 | C. | $\frac{9}{4}$ | D. | 9 |
6.在△ABC中,角A,B,C的对边分别为a,b,c,若a=2,b=sinA+cosA=$\sqrt{2}$,则△ABC的面积为( )
| A. | $\frac{\sqrt{6}+\sqrt{2}}{2}$ | B. | $\frac{\sqrt{6}+\sqrt{2}}{4}$ | C. | $\frac{\sqrt{3}+1}{4}$ | D. | $\frac{\sqrt{3}+1}{2}$ |
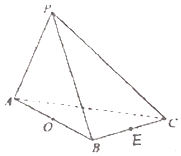 在三棱锥P-ABC中,△PAC和△PBC是边长为$\sqrt{2}$的等边三角形,AB=2,O是AB中点,E是BC中点.
在三棱锥P-ABC中,△PAC和△PBC是边长为$\sqrt{2}$的等边三角形,AB=2,O是AB中点,E是BC中点.