题目内容
5.若$A({3,\frac{π}{3}})$,$B({3,\frac{7π}{6}})$,则△AOB的面积为( )| A. | $\frac{{\sqrt{3}}}{4}$ | B. | 3 | C. | $\frac{9}{4}$ | D. | 9 |
分析 由A,B的极坐标,求得∠AOB,根据三角形的面积公式,即可求得△AOB的面积.
解答 解:由$A({3,\frac{π}{3}})$,$B({3,\frac{7π}{6}})$,则∠AOB=$\frac{7π}{6}$-$\frac{π}{3}$=$\frac{5π}{6}$,
∴△AOB的面积S=$\frac{1}{2}$×丨OA丨×丨OB丨sin∠AOB=$\frac{1}{2}$×3×3×$\frac{1}{2}$=$\frac{9}{4}$,
∴△AOB的面积$\frac{9}{4}$,
故选C.
点评 本题考查极坐标的应用,考查三角形的面积,考查计算能力,属于基础题.

练习册系列答案
 一课一练课时达标系列答案
一课一练课时达标系列答案 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
16.已知$tan({π-α})=\frac{3}{4},α∈({\frac{π}{2},π})$,则cosα=( )
| A. | $-\frac{4}{5}$ | B. | $\frac{4}{5}$ | C. | $-\frac{3}{5}$ | D. | $\frac{3}{5}$ |
14.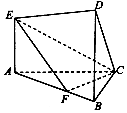 在如图所示的几何体中,EA⊥平面ABC,DB∥EA,AC⊥BC,且BC=BD=3,AE=2,AC=3$\sqrt{2}$,AF=2FB
在如图所示的几何体中,EA⊥平面ABC,DB∥EA,AC⊥BC,且BC=BD=3,AE=2,AC=3$\sqrt{2}$,AF=2FB
(1)求证:CF⊥EF;
(2)求二面角D-CE-F的余弦值.
 在如图所示的几何体中,EA⊥平面ABC,DB∥EA,AC⊥BC,且BC=BD=3,AE=2,AC=3$\sqrt{2}$,AF=2FB
在如图所示的几何体中,EA⊥平面ABC,DB∥EA,AC⊥BC,且BC=BD=3,AE=2,AC=3$\sqrt{2}$,AF=2FB(1)求证:CF⊥EF;
(2)求二面角D-CE-F的余弦值.
15.执行如图所示的程序框图,若输出k的值为6,则判断框内可填入的条件是( )


| A. | S>$\frac{1}{2}$ | B. | S>$\frac{3}{5}$ | C. | S>$\frac{7}{10}$ | D. | S>$\frac{4}{5}$ |