题目内容
6.在△ABC中,角A,B,C的对边分别为a,b,c,若a=2,b=sinA+cosA=$\sqrt{2}$,则△ABC的面积为( )| A. | $\frac{\sqrt{6}+\sqrt{2}}{2}$ | B. | $\frac{\sqrt{6}+\sqrt{2}}{4}$ | C. | $\frac{\sqrt{3}+1}{4}$ | D. | $\frac{\sqrt{3}+1}{2}$ |
分析 利用已知条件求出A,通过正弦定理求出B,然后求解C,利用三角形的面积公式求解即可.
解答 解:在△ABC中,角A,B,C的对边分别为a,b,c,若a=2,b=sinA+cosA=$\sqrt{2}$,
可得$\sqrt{2}$sin(A+$\frac{π}{4}$)=$\sqrt{2}$,可得A=$\frac{π}{4}$,
由正弦定理可得:sinB=$\frac{bsinA}{a}$=$\frac{\sqrt{2}×\frac{\sqrt{2}}{2}}{2}$=$\frac{1}{2}$,
∵a>b,∴A>B,可得B=$\frac{π}{6}$,所以C=$\frac{7π}{12}$,
则△ABC的面积为:$\frac{1}{2}absinC$=$\frac{1}{2}×2×\sqrt{2}×sin\frac{7π}{12}$=$\frac{\sqrt{2}(\sqrt{6}+\sqrt{2})}{4}$=$\frac{\sqrt{3}+1}{2}$.
故选:D.
点评 本题考查正弦定理的应用,三角形的面积公式的应用,注意正弦定理以及三角形边角关系的应用,是易错点.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
16.已知$tan({π-α})=\frac{3}{4},α∈({\frac{π}{2},π})$,则cosα=( )
| A. | $-\frac{4}{5}$ | B. | $\frac{4}{5}$ | C. | $-\frac{3}{5}$ | D. | $\frac{3}{5}$ |
14.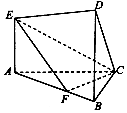 在如图所示的几何体中,EA⊥平面ABC,DB∥EA,AC⊥BC,且BC=BD=3,AE=2,AC=3$\sqrt{2}$,AF=2FB
在如图所示的几何体中,EA⊥平面ABC,DB∥EA,AC⊥BC,且BC=BD=3,AE=2,AC=3$\sqrt{2}$,AF=2FB
(1)求证:CF⊥EF;
(2)求二面角D-CE-F的余弦值.
 在如图所示的几何体中,EA⊥平面ABC,DB∥EA,AC⊥BC,且BC=BD=3,AE=2,AC=3$\sqrt{2}$,AF=2FB
在如图所示的几何体中,EA⊥平面ABC,DB∥EA,AC⊥BC,且BC=BD=3,AE=2,AC=3$\sqrt{2}$,AF=2FB(1)求证:CF⊥EF;
(2)求二面角D-CE-F的余弦值.
15.执行如图所示的程序框图,若输出k的值为6,则判断框内可填入的条件是( )


| A. | S>$\frac{1}{2}$ | B. | S>$\frac{3}{5}$ | C. | S>$\frac{7}{10}$ | D. | S>$\frac{4}{5}$ |