题目内容
1.已知函数$f(x)=\left\{\begin{array}{l}-2x-{x^2},x≤0\\|{lgx}|,x>0\end{array}\right.$,若a<b<c<d,且f(a)=f(b)=f(c)=f(d),则a+b+c+2d的取值范围是( )| A. | $({3,\frac{201}{10}})$ | B. | $({1,\frac{181}{10}})$ | C. | $({2\sqrt{2},+∞})$ | D. | $({2\sqrt{2}-2,+∞})$ |
分析 设f(a)=f(b)=f(c)=f(d)=k,推出a,b为方程x2+2x+k=0的不同实根,得到a+b=-2,通过|lgc|=|lgd|推出1<d<10,然后求解a+b+c+2d∈(1,$\frac{181}{10}$).
解答 解:不妨设f(a)=f(b)=f(c)=f(d)=k,
则:a,b,c,d为f(x)=k的四个不同的实数根,
于是a,b为方程x2+2x+k=0的不同实根,所以a+b=-2,
由|lgc|=|lgd|可知:且由于0<lgd<1,可知1<d<10,于是c+2d=2d+$\frac{1}{d}$∈(3,$\frac{201}{10}$),
于是:a+b+c+2d∈(1,$\frac{181}{10}$).
故选:B.
点评 本题考查函数的零点与方程根的关系,考查转化思想以及计算能力.

练习册系列答案
相关题目
16.已知$tan({π-α})=\frac{3}{4},α∈({\frac{π}{2},π})$,则cosα=( )
| A. | $-\frac{4}{5}$ | B. | $\frac{4}{5}$ | C. | $-\frac{3}{5}$ | D. | $\frac{3}{5}$ |
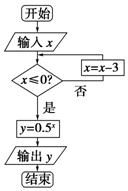 如图所示的程序框图,当输入x的值为3时,则其输出的结果是1.
如图所示的程序框图,当输入x的值为3时,则其输出的结果是1.