题目内容
在面积为7的△ABC的边AB上任取一点P，则△PBC的面积小于
的概率是 ．
| 7 |
| 3 |
考点：几何概型
专题：计算题,概率与统计
分析：在三角形ABC内部取一点P，要满足得到的三角形PBC的面积是原三角形面积的
，根据几何关系求解出它们的比例即可．
| 1 |
| 3 |
解答：
解：记事件A={△PBC的面积大于
}，
基本事件是三角形ABC的面积，（如图）
事件A的几何度量为图中阴影部分的面积（D、E分别是三角形的边上的三等分点），
∵△ADE∽△ABC，且相似比为
，
∴阴影部分的面积是整个三角形面积的
，
∴P（A）=
，
∴△PBC的面积小于
的概率是1-P（A）=1-
=
．
故答案为：
．
| 7 |
| 3 |
基本事件是三角形ABC的面积，（如图）
事件A的几何度量为图中阴影部分的面积（D、E分别是三角形的边上的三等分点），
∵△ADE∽△ABC，且相似比为
| 2 |
| 3 |
∴阴影部分的面积是整个三角形面积的
| 4 |
| 9 |
∴P（A）=
| 4 |
| 9 |
∴△PBC的面积小于
| 7 |
| 3 |
| 4 |
| 9 |
| 5 |
| 9 |
故答案为：
| 5 |
| 9 |
点评：本题考查了几何概型，解答此题的关键在于明确测度比是面积比．对于几何概型常见的测度是长度之比，面积之比，体积之比，角度之比，要根据题意合理的判断和选择是哪一种测度进行求解．属于中档题．
练习册系列答案
能力评价系列答案
唐印文化课时测评系列答案
相关题目
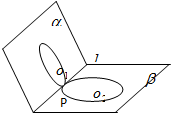如图，在120°二面角α-l-β内半径为1的圆O1与半径为2的圆α分别在半平面α、l内，且与棱l切于同一点P，则以圆O1与圆f（x）=2sin（ωx-已知|2
+
|=5，|2
-
|=3，且（
+
）⊥（
-2
），则
与
的夹角为（ ）
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| A、0 | ||
B、
| ||
C、
| ||
| D、π |
设向量
=（1，2），
=（-2，y），若
∥
，则|3
+
|等于（ ）
| a |
| b |
| a |
| b |
| a |
| b |
A、
| ||
B、
| ||
C、
| ||
D、
|