题目内容
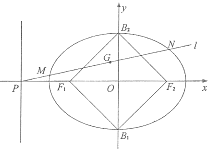 如图,已知椭圆C的中心在原点,焦点在x轴上,以两个焦点和短轴的两个端点为顶点的四边形F1B1F2B2是一个面积为8的正方形(记为Q ).
如图,已知椭圆C的中心在原点,焦点在x轴上,以两个焦点和短轴的两个端点为顶点的四边形F1B1F2B2是一个面积为8的正方形(记为Q ).(Ⅰ)求椭圆C的方程;
(Ⅱ)设点P是椭圆C的左准线与x轴的交点,过点P的直线l与椭圆C相交于M,N两点、.当线段MN的中点G落在正方形Q内(包括边界)时,求直线L的斜率的取值范围.
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线中的最值与范围问题
分析:(I)设椭圆的标准方程为
+
=1(a>b>0),由于a2=8,b=c,a2=b2+c2,解得即可得出.
(II)椭圆C的左准线方程为x=-4,可得点P的坐标为(-4,0).由于直线l的斜率k存在,可设直线l的方程为y=k(x+4).设点M,N的坐标分别为(x1,y1),(x2,y2),线段MN的中点为G(x0,y0),直线方程与椭圆方程联立可得(1+2k2)x2+16k2x+32k2-8=0.由△>0解得-
<k<
.利用根与系数的关系及其中点坐标公式可得,x0=
=
,y0=
.由于x0≤0,点G不可能在y轴的右边.直线F1B2,F1B1方程分别为y=x+2,y=-x-2.点G在正方形内(包括边界)的充要条件为
,解出即可.
| x2 |
| a2 |
| y2 |
| b2 |
(II)椭圆C的左准线方程为x=-4,可得点P的坐标为(-4,0).由于直线l的斜率k存在,可设直线l的方程为y=k(x+4).设点M,N的坐标分别为(x1,y1),(x2,y2),线段MN的中点为G(x0,y0),直线方程与椭圆方程联立可得(1+2k2)x2+16k2x+32k2-8=0.由△>0解得-
| ||
| 2 |
| ||
| 2 |
| x1+x2 |
| 2 |
| -8k2 |
| 1+2k2 |
| 4k |
| 1+2k2 |
|
解答:
解:(I)设椭圆的标准方程为
+
=1(a>b>0),
∵a2=8,b=c,a2=b2+c2,解得b2=4,
∴椭圆C的标准方程为
+
=1.
(II)椭圆C的左准线方程为x=-4,∴点P的坐标为(-4,0).
由于直线l的斜率k存在,可设直线l的方程为y=k(x+4).
设点M,N的坐标分别为(x1,y1),(x2,y2),线段MN的中点为G(x0,y0),联立
,
可得(1+2k2)x2+16k2x+32k2-8=0.①
由△=(16k2)2-4(1+2k2)(32k2-8)>0解得-
<k<
.②
∴x1+x2=
,x0=
=
,y0=k(x0+4)=
.
∵x0≤0,所以点G不可能在y轴的右边.
又直线F1B2,F1B1方程分别为y=x+2,y=-x-2
∴点G在正方形内(包括边界)的充要条件为
,
即
化为
,解得-
≤k≤
.
满足②.∴直线l的斜率的取值范围是[-
,
].
| x2 |
| a2 |
| y2 |
| b2 |
∵a2=8,b=c,a2=b2+c2,解得b2=4,
∴椭圆C的标准方程为
| x2 |
| 8 |
| y2 |
| 4 |
(II)椭圆C的左准线方程为x=-4,∴点P的坐标为(-4,0).
由于直线l的斜率k存在,可设直线l的方程为y=k(x+4).
设点M,N的坐标分别为(x1,y1),(x2,y2),线段MN的中点为G(x0,y0),联立
|
可得(1+2k2)x2+16k2x+32k2-8=0.①
由△=(16k2)2-4(1+2k2)(32k2-8)>0解得-
| ||
| 2 |
| ||
| 2 |
∴x1+x2=
| -16k2 |
| 1+2k2 |
| x1+x2 |
| 2 |
| -8k2 |
| 1+2k2 |
| 4k |
| 1+2k2 |
∵x0≤0,所以点G不可能在y轴的右边.
又直线F1B2,F1B1方程分别为y=x+2,y=-x-2
∴点G在正方形内(包括边界)的充要条件为
|
即
|
|
| ||
| 2 |
| ||
| 2 |
满足②.∴直线l的斜率的取值范围是[-
| ||
| 2 |
| ||
| 2 |
点评:本题考查了椭圆的标准方程及其性质、直线与椭圆相交问题转化为方程联立可得根与系数的关系、中点坐标公式、线性规划的有关知识,考查了推理能力与计算能力,属于难题.

练习册系列答案
相关题目
已知|2
+
|=5,|2
-
|=3,且(
+
)⊥(
-2
),则
与
的夹角为( )
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| A、0 | ||
B、
| ||
C、
| ||
| D、π |
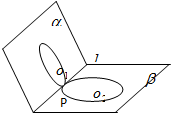 如图,在120°二面角α-l-β内半径为1的圆O1与半径为2的圆α分别在半平面α、l内,且与棱l切于同一点P,则以圆O1与圆f(x)=2sin(ωx-
如图,在120°二面角α-l-β内半径为1的圆O1与半径为2的圆α分别在半平面α、l内,且与棱l切于同一点P,则以圆O1与圆f(x)=2sin(ωx-