题目内容
函数f(x)=ax3+bx2+cx+d(x∈R)的图象经过原点,且f(-1)=2和f(1)=-2分别是函数f(x)的极大值和极小值.
(Ⅰ)求a,b,c,d;
(Ⅱ)过点A(1,-3)作曲线y=f(x)的切线,求所得切线方程.
(Ⅰ)求a,b,c,d;
(Ⅱ)过点A(1,-3)作曲线y=f(x)的切线,求所得切线方程.
考点:利用导数研究函数的极值,利用导数研究曲线上某点切线方程
专题:导数的综合应用
分析:(Ⅰ)由于函数f(x)的图象经过原点,可得f(0)=d=0.f(-1)=2和f(1)=-2分别是函数f(x)的极大值和极小值,可得f′(-1)=f′(1)=0,解出即可.
(II)设切点为M(x0,x03-3x0).可得切线方程为:y-(x03-3x0)=(3x02-3)(x-x0),把点A(1,-3)代入解出即可.
(II)设切点为M(x0,x03-3x0).可得切线方程为:y-(x03-3x0)=(3x02-3)(x-x0),把点A(1,-3)代入解出即可.
解答:
解:(Ⅰ)∵函数f(x)的图象经过原点,
∴f(0)=d=0.
∵f(-1)=2和f(1)=-2分别是函数f(x)的极大值和极小值.
∴f'(x)=3ax2+2bx+c=3a(x+1)(x-1)=3ax2-3a,
∴b=0,c=-3a,
∴f(x)=ax3-3ax,
又∵f(-1)=2,f(1)=-2,
∴a=1
经检验,a=1,b=0,c=-3,d=0
即:f(x)=x3-3x.
(Ⅱ)设切点为M(x0,x03-3x0).
则切线方程为:y-(x03-3x0)=(3x02-3)(x-x0),
把点A(1,-3)代入可得-3-(x03-3x0)=(3x02-3)(1-x0),
即:2x03-3x02=0,
解得x0=0或x0=
.
∴切线为y=-3x和y=
x-
.
∴f(0)=d=0.
∵f(-1)=2和f(1)=-2分别是函数f(x)的极大值和极小值.
∴f'(x)=3ax2+2bx+c=3a(x+1)(x-1)=3ax2-3a,
∴b=0,c=-3a,
∴f(x)=ax3-3ax,
又∵f(-1)=2,f(1)=-2,
∴a=1
经检验,a=1,b=0,c=-3,d=0
即:f(x)=x3-3x.
(Ⅱ)设切点为M(x0,x03-3x0).
则切线方程为:y-(x03-3x0)=(3x02-3)(x-x0),
把点A(1,-3)代入可得-3-(x03-3x0)=(3x02-3)(1-x0),
即:2x03-3x02=0,
解得x0=0或x0=
| 3 |
| 2 |
∴切线为y=-3x和y=
| 15 |
| 4 |
| 27 |
| 4 |
点评:本题考查了利用导数研究函数的极值、切线的斜率、切线方程,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
已知|2
+
|=5,|2
-
|=3,且(
+
)⊥(
-2
),则
与
的夹角为( )
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| A、0 | ||
B、
| ||
C、
| ||
| D、π |
设向量
=(1,2),
=(-2,y),若
∥
,则|3
+
|等于( )
| a |
| b |
| a |
| b |
| a |
| b |
A、
| ||
B、
| ||
C、
| ||
D、
|
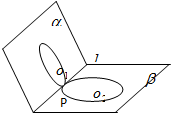 如图,在120°二面角α-l-β内半径为1的圆O1与半径为2的圆α分别在半平面α、l内,且与棱l切于同一点P,则以圆O1与圆f(x)=2sin(ωx-
如图,在120°二面角α-l-β内半径为1的圆O1与半径为2的圆α分别在半平面α、l内,且与棱l切于同一点P,则以圆O1与圆f(x)=2sin(ωx-
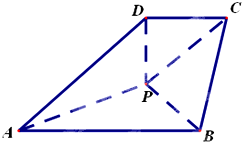 四棱锥P-ABCD如图放置,AB∥CD,BC⊥CD,AB=BC=2,CD=PD=1,△PAB为等边三角形.
四棱锥P-ABCD如图放置,AB∥CD,BC⊥CD,AB=BC=2,CD=PD=1,△PAB为等边三角形.