题目内容
 如图,四棱锥P-ABCD中,底面ABCD为是矩形,PA⊥底面ABCD,E为棱PD的中点,AP=2,AD=2
如图,四棱锥P-ABCD中,底面ABCD为是矩形,PA⊥底面ABCD,E为棱PD的中点,AP=2,AD=2| 3 |
| 3 |
(Ⅰ)求证:PB∥平面AEC;
(Ⅱ)求直线AE与平面PAC所成角的正弦值.
考点:直线与平面所成的角,直线与平面平行的判定
专题:空间位置关系与距离
分析:(Ⅰ)由三棱锥体积求CD的长度,建立坐标系,得到
∥
,可证PB∥平面AEC;
(Ⅱ)设平面PAC的一个法向量
=(x,y,z),利用
•
=0,且
•
=0求一个法向量,利用
,
的数量积求它们的夹角余弦值.
| PB |
| EO |
(Ⅱ)设平面PAC的一个法向量
| n |
| AP |
| n |
| AC |
| n |
| AE |
| n |
解答:
 解:( I)由VE-ACD=
解:( I)由VE-ACD=
•
AD•CD•
PA=
,得CD=3,---------------------(2分)
如图所示,以A为坐标原点,
方向为x轴正方向,建立空间直角坐标系由已知,A(0,0,0),B(3,0,0),C(3,2
,0),D(0,2
,0),P(0,0,2)E(0,
,1)
取AC中点O,O(
,
,0),
则
=(3,0,-2),
=(
,0,-1),
=2
,
∥
,
即PB∥EO---------------------(4分)
∵EO?平面AEC,PB?平面AEC
∴PB∥平面AEC---------------------(6分)
( II)
=(0,
,1),
=(0,0,2),
=(3,2
,0)
设平面PAC的一个法向量
=(x,y,z)
则
⊥
,且
⊥
,即
•
=0,且
•
=0
∴
,令x=1,解得
=(1,-
,0)--------------------(8分)
cos<
,
>=
=-
---------------------(10分)
直AE与平面PAC所成角的正弦值为
---------------------(12分)
 解:( I)由VE-ACD=
解:( I)由VE-ACD=| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
如图所示,以A为坐标原点,
| AB |
| 3 |
| 3 |
| 3 |
取AC中点O,O(
| 3 |
| 2 |
| 3 |
则
| PB |
| EO |
| 3 |
| 2 |
| PB |
| EO |
| PB |
| EO |
即PB∥EO---------------------(4分)
∵EO?平面AEC,PB?平面AEC
∴PB∥平面AEC---------------------(6分)
( II)
| AE |
| 3 |
| AP |
| AC |
| 3 |
设平面PAC的一个法向量
| n |
则
| AP |
| n |
| AC |
| n |
| AP |
| n |
| AC |
| n |
∴
|
| n |
| ||
| 2 |
cos<
| AE |
| n |
-
| ||||||
|
3
| ||
| 14 |
直AE与平面PAC所成角的正弦值为
3
| ||
| 14 |
点评:本题考查了线面平行的判定以及线面角的求法;本题借助于向量解答,体现了向量的工具性,属于中档题.

练习册系列答案
相关题目
已知|2
+
|=5,|2
-
|=3,且(
+
)⊥(
-2
),则
与
的夹角为( )
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| A、0 | ||
B、
| ||
C、
| ||
| D、π |
如函数f(x)=-x2+2ax与函数g(x)=
在区间(2,5]上都是减函数,则实数a的取值范围为( )
| a |
| x+1 |
| A、(-2,0] |
| B、(-2,0) |
| C、(0,2) |
| D、(0,2] |
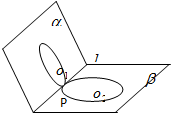 如图,在120°二面角α-l-β内半径为1的圆O1与半径为2的圆α分别在半平面α、l内,且与棱l切于同一点P,则以圆O1与圆f(x)=2sin(ωx-
如图,在120°二面角α-l-β内半径为1的圆O1与半径为2的圆α分别在半平面α、l内,且与棱l切于同一点P,则以圆O1与圆f(x)=2sin(ωx-