题目内容
已知函数f(x)=sinωx•sin(
-φ)-sin(
+ωx)sin(π+φ)是R上的偶函数,其中ω>0,0≤φ≤π,其图象关于点M(
,0)对称,且在区间[0,
]上是单调函数,求φ和ω的值.
| π |
| 2 |
| π |
| 2 |
| 3π |
| 4 |
| π |
| 2 |
考点:两角和与差的正弦函数,正弦函数的单调性
专题:三角函数的求值
分析:由条件利用诱导公式、两角和的正弦公式可得f(x)=sin(ωx+φ),根据它是偶函数,结合φ的范围,可得φ=
,f(x)=cosωx.再根据cos(ω•
)=0,求得ω 的范围,再由f(x)=cosωx 在区间[0,
]上是单调函数,可得ω•
≤π,从而求得ω的值.
| π |
| 2 |
| 3π |
| 4 |
| π |
| 2 |
| π |
| 2 |
解答:
解:∵函数f(x)=sinωx•sin(
-φ)-sin(
+ωx)sin(π+φ)
=sinωx•cosφ+cosωx•sinφ=sin(ωx+φ)是偶函数,
∴φ=2kπ+
,k∈z.
再结合0≤φ≤π,可得φ=
,故f(x)=sin(ωx+
)=cosωx.
再根据函数f(x)的图象关于点M(
,0)对称,可得cos(ω•
)=0,
∴ω•
=nπ+
,n∈z,即ω=
,∴ω=2,5,8,…
再由f(x)=cosωx 在区间[0,
]上是单调函数,可得ω•
≤π,∴ω≤2,∴ω=2.
综上可得,ω=2,φ=
.
| π |
| 2 |
| π |
| 2 |
=sinωx•cosφ+cosωx•sinφ=sin(ωx+φ)是偶函数,
∴φ=2kπ+
| π |
| 2 |
再结合0≤φ≤π,可得φ=
| π |
| 2 |
| π |
| 2 |
再根据函数f(x)的图象关于点M(
| 3π |
| 4 |
| 3π |
| 4 |
∴ω•
| 3π |
| 4 |
| π |
| 2 |
| 4n+2 |
| 3 |
再由f(x)=cosωx 在区间[0,
| π |
| 2 |
| π |
| 2 |
综上可得,ω=2,φ=
| π |
| 2 |
点评:本题主要考查诱导公式、两角和的正弦公式、余弦函数的图象的对称性、余弦函数的单调性,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
函数f(x)=tx2+4tx+1(t>5),若x1>x2,x1+x2=1-t,则( )
| A、f(x1)>f(x2) |
| B、f(x1)<f(x2) |
| C、f(x1)=f(x2) |
| D、f(x1),f(x2)大小关系不能确定 |

 如图,在四棱锥P-ABCD中,底面ABCD是边长为1的正方形,PA⊥平面ABCD,PA=AB,M、N分别是线段PB、AC上的动点,且不与端点重合,PM=AN.
如图,在四棱锥P-ABCD中,底面ABCD是边长为1的正方形,PA⊥平面ABCD,PA=AB,M、N分别是线段PB、AC上的动点,且不与端点重合,PM=AN.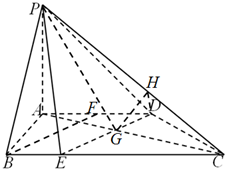 如图,在四棱锥PE=3中,AE=
如图,在四棱锥PE=3中,AE=