题目内容
在△ABC，AB=AC，点D在边BC上，点P在边AD上，已知BD=2DC，∠ABP=∠CAP．求证：∠CPD=
∠BAC．
| 1 |
| 2 |
考点：两直线的夹角与到角问题,相似三角形的判定
专题：立体几何
分析：如图所示，建立直角坐标系．不妨设D（4，0），C（6，0），A（3，a）．设
=λ
，可得
=
+λ
=（4-λ，λa）．利用向量计算公式可得kBP=
，kBA=
．因此tan∠ABP=
=
．同理可得tan∠DAC=
=
，利用∠ABP=∠DAC，可得λ=
．由于
tan∠BAC=-tan2∠ABC=
．tan∠DPC=
=
．可得tan2∠DPC=
．即可证明．
| DP |
| DA |
| BP |
| BD |
| DA |
| λa |
| 4-λ |
| a |
| 3 |
| kBA-kBP |
| 1+kBA•kBP |
| 4a-4λa |
| 12-3λ+λa2 |
| kAC-kAD |
| 1+kACkAD |
| 2a |
| 3+a2 |
| 2a2-6 |
| 3+3a2 |
tan∠BAC=-tan2∠ABC=
| -2tan∠ABC |
| 1-tan2∠ABC |
| kPC-kAD |
| 1+kPC•kAD |
| 3 |
| a |
| 2tan∠DPC |
| 1-tan2∠DPC |
解答：
证明：如图所示，建立直角坐标系．
不妨设D（4，0），C（6，0），A（3，a）．
设
=λ
，则
=
+λ
=（4-λ，λa）．
∴kBP=
，kBA=
．
∴tan∠ABP=
=
．
∵kAC=-
，kAD=-a．
∴tan∠DAC=
=
，
∵∠ABP=∠DAC，
∴
=
，化为λ=
．
tan∠BAC=-tan2∠ABC=
=
．
kPC=
=
．
tan∠DPC=
=
．
∴tan2∠DPC=
=
．
∴tan2∠DPC=tan∠BAC．
∴∠DPC=
∠BAC．
不妨设D（4，0），C（6，0），A（3，a）．设
| DP |
| DA |
| BP |
| BD |
| DA |
∴kBP=
| λa |
| 4-λ |
| a |
| 3 |
∴tan∠ABP=
| kBA-kBP |
| 1+kBA•kBP |
| 4a-4λa |
| 12-3λ+λa2 |
∵kAC=-
| a |
| 3 |
∴tan∠DAC=
| kAC-kAD |
| 1+kACkAD |
| 2a |
| 3+a2 |
∵∠ABP=∠DAC，
∴
| 4a-4λa |
| 12-3λ+λa2 |
| 2a |
| 3+a2 |
| 2a2-6 |
| 3+3a2 |
tan∠BAC=-tan2∠ABC=
| -2tan∠ABC |
| 1-tan2∠ABC |
| 6a |
| a2-9 |
kPC=
| -λa |
| 2+λ |
| 3-a2 |
| 4a |
tan∠DPC=
| kPC-kAD |
| 1+kPC•kAD |
| 3 |
| a |
∴tan2∠DPC=
| 2tan∠DPC |
| 1-tan2∠DPC |
| 6a |
| a2-9 |
∴tan2∠DPC=tan∠BAC．
∴∠DPC=
| 1 |
| 2 |
点评：本题考查了通过建立直角坐标系利用斜率计算公式、到角公式、正切公式、诱导公式等基础知识与基本技能方法，考查了推理能力与计算能力，属于难题．
练习册系列答案
相关题目
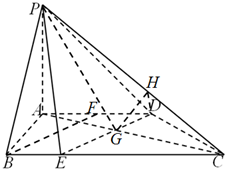如图，在四棱锥PE=3中，AE=