题目内容
16.双曲线C的一条渐近线方程是:x-2y=0,且曲线C过点$(2\sqrt{2},1)$.(1)求双曲线C的方程;
(2)设曲线C的左、右顶点分别是A1、A2,P为曲线C上任意一点,PA1、PA2分别与直线l:x=1交于M、N,求|MN|的最小值.
分析 (1)根据三角形的渐近线方程利用待定系数法进行求解即可.
(2)联立方程组求出交点坐标,结合两点间的距离公式进行求解即可.
解答 解:(1)由渐近线方程可知,双曲线C的方程为x2-4y2=k,把$(2\sqrt{2},1)$代入可得k=4,
所以双曲线方程为$\frac{x^2}{4}-{y^2}=1$.(4分)
(2)由双曲线的对称性可知,P在右支上时,|MN|取最小值.
由上可得A1(-2,0),A2(2,0),根据双曲线方程可得$\frac{y}{x-2}•\frac{y}{x+2}=\frac{1}{4}$,
所以设直线PA1、PA2的斜率分别为k1、k2(k1、k2>0),
则${k_1}{k_2}=\frac{1}{4}$.PA1的方程为y=k1(x+2),令x=1,解得M(1,3k1)
,PA2的方程为y=k2(x-2),令x=1,解得N(1,-k2),
所以|MN|=$|{3{k_1}-(-{k_2})}|=3{k_1}+{k_2}≥2\sqrt{3{k_1}{k_2}}=\sqrt{3}$.
当且仅当3k1=k2,即${k_1}=\frac{{\sqrt{3}}}{6},{k_2}=\frac{{\sqrt{3}}}{2}$时等号成立.(12分)
点评 本题主要考查双曲线方程的求解以及两点间距离的计算,考查学生的运算能力.

练习册系列答案
相关题目
8.如图,给出的是计算1+$\frac{1}{3}$+$\frac{1}{5}$+…+$\frac{1}{99}$+$\frac{1}{101}$的值的一个程序框图,判断框内应填入的条件是( )

| A. | i<101? | B. | i>101? | C. | i≤101? | D. | i≥101? |
8.设p:log2x<0,q:2x≥2,则p是¬q的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
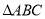 中,
中,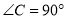 ,点
,点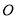 在
在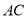 上,以
上,以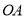 为半径的
为半径的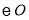 交
交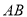 于点
于点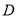 ,
,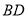 的垂直平分线交
的垂直平分线交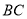 于点
于点 ,交
,交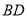 于点
于点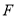 ,连接
,连接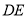 .
.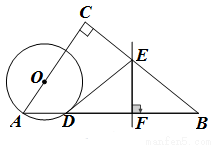
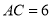 ,
,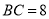 ,
, ,求线段
,求线段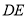 的长.
的长.