题目内容
11.求函数y=sinx的图象,x∈[0,π]与函数y=cosx的图象,x∈[0,π]图象围成的图形面积为$\sqrt{2}$.分析 方法一:由图形的对称性质可得,方法二,S=${∫}_{\frac{π}{4}}^{π}$sinxdx-${∫}_{\frac{π}{4}}^{\frac{π}{2}}$cosxdx,分别根据定积分的定义即可求出.
解答 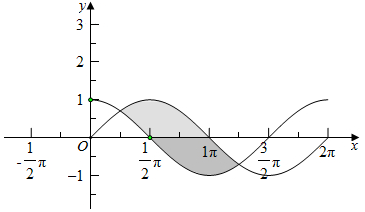 解:方法一:由图形的对称性质可得,$S=\frac{1}{2}\int_{\frac{π}{4}}^{\frac{5π}{4}}{(sinx-cosx)dx=\frac{1}{2}}(cos\frac{π}{4}+sin\frac{π}{4})-\frac{1}{2}(cos\frac{5π}{4}+sin\frac{5π}{4})=\sqrt{2}$.
解:方法一:由图形的对称性质可得,$S=\frac{1}{2}\int_{\frac{π}{4}}^{\frac{5π}{4}}{(sinx-cosx)dx=\frac{1}{2}}(cos\frac{π}{4}+sin\frac{π}{4})-\frac{1}{2}(cos\frac{5π}{4}+sin\frac{5π}{4})=\sqrt{2}$.
方法二:由图图可知,S=${∫}_{\frac{π}{4}}^{π}$sinxdx-${∫}_{\frac{π}{4}}^{\frac{π}{2}}$cosxdx=(1+$\frac{\sqrt{2}}{2}$)-(1-$\frac{\sqrt{2}}{2}$)=$\sqrt{2}$
故答案为:$\sqrt{2}$
点评 本题考查了定积分在几何中的应用,以及正弦余弦函数的图象,属于基础题.

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
3.已知0<θ<$\frac{π}{2}$,f(θ)=1+m+m($\frac{cosθ-1}{sinθ}$)+$\frac{sinθ-1}{cosθ}$(m>0),则使得f(θ)有最大值时的m的取值范围是( )
| A. | ($\frac{1}{2}$,2) | B. | ($\frac{1}{3}$,3) | C. | [1,3] | D. | [$\frac{1}{4}$,1] |
20.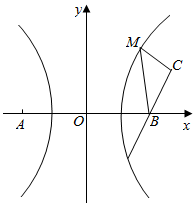 如图,M是以A、B为焦点的双曲线x2-y2=2右支上任一点,若点M到点C(3,1)与点B的距离之和为S,则S的取值范围是( )
如图,M是以A、B为焦点的双曲线x2-y2=2右支上任一点,若点M到点C(3,1)与点B的距离之和为S,则S的取值范围是( )
 如图,M是以A、B为焦点的双曲线x2-y2=2右支上任一点,若点M到点C(3,1)与点B的距离之和为S,则S的取值范围是( )
如图,M是以A、B为焦点的双曲线x2-y2=2右支上任一点,若点M到点C(3,1)与点B的距离之和为S,则S的取值范围是( )| A. | [$\sqrt{26}$+$\sqrt{2}$,+∞) | B. | [$\sqrt{26}$-$2\sqrt{2}$,+∞) | C. | [$\sqrt{26}$-$2\sqrt{2}$,$\sqrt{26}$+$2\sqrt{2}$) | D. | [$\sqrt{26}$-$\sqrt{2}$,+∞) |
20.已知△ABC的内切圆与边AB,AC,BC相切于点P,Q,R,若|CR|=1,|AB|=2,则动点C的轨迹曲线的离心率为( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | 1 | D. | 2 |