题目内容
1.已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{3}}{2}$,且与y轴正半轴的交点为(0,1)(Ⅰ)求椭圆的方程;
(Ⅱ)若直线l与C交于A、B两点,AB=2,求△AOB的面积的最大值.
分析 (Ⅰ)由题意知e=$\frac{c}{a}$=$\frac{\sqrt{3}}{2}$,b=1;从而解得a=2,b=1,c=$\sqrt{3}$;从而写出椭圆的方程;
(Ⅱ)设直线l的方程为y=kx+b,从而可得(1+4k2)x2+8kbx+4b2-4=0,设A(x1,y1),B(x2,y2),从而可得|AB|=$\sqrt{1+{k}^{2}}$•$\sqrt{({x}_{1}+{x}_{2})^{2}-4{x}_{1}{x}_{2}}$=$\sqrt{1+{k}^{2}}$•$\sqrt{\frac{64{k}^{2}+16-16{b}^{2}}{(1+4{k}^{2})^{2}}}$=2,从而化简方程可得4b2=$\frac{12{k}^{2}+3}{1+{k}^{2}}$;代入面积公式S=$\frac{1}{2}$•2•$\frac{|b|}{\sqrt{1+{k}^{2}}}$=$\frac{1}{2}$$\sqrt{\frac{4{b}^{2}}{1+{k}^{2}}}$=$\frac{1}{2}$$\sqrt{\frac{12{k}^{2}+3}{(1+{k}^{2})^{2}}}$,从而求最值.
解答 解:(Ⅰ)∵椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{3}}{2}$,
∴e=$\frac{c}{a}$=$\frac{\sqrt{3}}{2}$;
∵与y轴正半轴的交点为(0,1),
∴b=1;
∴a=2,b=1,c=$\sqrt{3}$;
故椭圆C的方程为$\frac{{x}^{2}}{4}$+y2=1;
(Ⅱ)设直线l的方程为y=kx+b,
与椭圆方程联立消元化简可得,
(1+4k2)x2+8kbx+4b2-4=0,
设A(x1,y1),B(x2,y2),
则x1+x2=-$\frac{8kb}{1+4{k}^{2}}$,x1x2=$\frac{4{b}^{2}-4}{4{k}^{2}+1}$;
|AB|=$\sqrt{1+{k}^{2}}$•$\sqrt{({x}_{1}+{x}_{2})^{2}-4{x}_{1}{x}_{2}}$
=$\sqrt{1+{k}^{2}}$•$\sqrt{\frac{64{k}^{2}+16-16{b}^{2}}{(1+4{k}^{2})^{2}}}$=2,
∴2$\sqrt{1+{k}^{2}}$•$\sqrt{1+4{k}^{2}-{b}^{2}}$=(1+4k2)2,
∴12k2+3=4b2(1+k2),
∴4b2=$\frac{12{k}^{2}+3}{1+{k}^{2}}$;
S=$\frac{1}{2}$•2•$\frac{|b|}{\sqrt{1+{k}^{2}}}$
=$\frac{1}{2}$$\sqrt{\frac{4{b}^{2}}{1+{k}^{2}}}$=$\frac{1}{2}$$\sqrt{\frac{12{k}^{2}+3}{(1+{k}^{2})^{2}}}$,
∵$\frac{12{k}^{2}+3}{(1+{k}^{2})^{2}}$=$\frac{12}{1+{k}^{2}}$-$\frac{9}{(1+{k}^{2})^{2}}$=-9($\frac{1}{1+{k}^{2}}$-$\frac{2}{3}$)2+4,
∴当$\frac{1}{1+{k}^{2}}$=$\frac{2}{3}$,即k2=$\frac{3}{2}$时,有最大值4;
∴Smax=$\frac{1}{2}$×$\sqrt{4}$=1.
点评 本题考查了椭圆的方程的求法与圆锥曲线与直线的位置关系的应用,同时考查了学生的化简运算能力,属于中档题.

 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案| A. | 2 | B. | 4 | C. | 16 | D. | 0 |
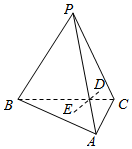 三棱锥P-ABC中,D、E分别是三角形PAC和三角形ABC的外心,则下列判断一定正确的是( )
三棱锥P-ABC中,D、E分别是三角形PAC和三角形ABC的外心,则下列判断一定正确的是( )| A. | DE∥PB | B. | 当AB=BC且PA=AC时DE∥PB | ||
| C. | 当且仅当AB=BC且PA=AC时,DE⊥AC | D. | DE⊥AC |
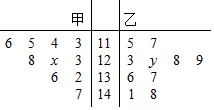 在某校统考中,甲、乙两班数学学科前10名的成绩如表:
在某校统考中,甲、乙两班数学学科前10名的成绩如表: