题目内容
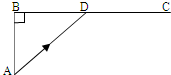 如图,已知海岛A与海岸公路BC的距离为50km,B、C间的距离为100km,从A到C,必须先坐船到BC上某一点D,船速为25km/h,再乘汽车,车速为50km/h.
如图,已知海岛A与海岸公路BC的距离为50km,B、C间的距离为100km,从A到C,必须先坐船到BC上某一点D,船速为25km/h,再乘汽车,车速为50km/h.设∠BAD=θ.记∠BAD=α(α为确定的锐角,满足tanα=
| 1 |
| 2 |
(1)试将由A到C所用时间t表示为θ的函数t(θ),并指出函数的定义域;
(2)问θ为多少时,使从A到C所用时间最少?并求出所用的最少时间.
考点:导数在最大值、最小值问题中的应用,解三角形的实际应用
专题:计算题,应用题,导数的综合应用
分析:(1)用θ表示出AD与BD,从而可以表示出DC,由路程除以速度得时间,建立起时间关于θ函数即可;
(2)对函数进行求导研究函数的单调性,借助三角函数的性质可得出当当θ=
时,用时最少,代入函数关系式求出最值即可.
(2)对函数进行求导研究函数的单调性,借助三角函数的性质可得出当当θ=
| π |
| 6 |
解答:
解:(1)AD=
,所以A到D所用时间t1=
,BD=50tanθ=
,
∴DC=100-BD=100-50tanθ=100-
,
所以D到C所用时间t2=2-
,
所以t(θ)=t1+t2=2+
,定义域为[0,α],α∈[0,
).
(2)t′(θ)=
=
令t'(θ)>0,则sinθ>
,即有
<θ<
,
由于∠BAD=α,则
<θ<α,t(θ)单调增;
令t'(θ)<0,则sinθ<
,即有0<θ<
,t(θ)单调减;
因此,θ=
,t(θ)取到最小值2+
.
答:当θ=
时,由A到C的时间t最少,最少时间为2+
小时.
| 50 |
| cosθ |
| 2 |
| cosθ |
| 50sinθ |
| cosθ |
∴DC=100-BD=100-50tanθ=100-
| 50sinθ |
| cosθ |
所以D到C所用时间t2=2-
| sinθ |
| cosθ |
所以t(θ)=t1+t2=2+
| 2-sinθ |
| cosθ |
| π |
| 2 |
(2)t′(θ)=
| -cos2θ+sinθ(2-sinθ) |
| cos2θ |
| 2sinθ-1 |
| cos2θ |
令t'(θ)>0,则sinθ>
| 1 |
| 2 |
| π |
| 6 |
| π |
| 2 |
由于∠BAD=α,则
| π |
| 6 |
令t'(θ)<0,则sinθ<
| 1 |
| 2 |
| π |
| 6 |
因此,θ=
| π |
| 6 |
| 3 |
答:当θ=
| π |
| 6 |
| 3 |
点评:本题考查在实际问题中建立三角函数模型,应用三角函数模型求解用时最少的问题,求解本题的关键是对问题进行细致分析得出符合条件的函数模型,本题在求最值时用到了导数研究单调性,用导数研究函数的单调性是一个非常方便的工具,遇到判断函数的单调性的问题时不妨优先考虑一下用导数.本题符号较多,运算较繁,极易出错,做题时要认真严谨.

练习册系列答案
相关题目
已知集合 A={y|y=2-x,x<0},集合 B={x|x≥0},则A∩B=( )
| A、(1,+∞) |
| B、[1,+∞) |
| C、(0,+∞) |
| D、[0,+∞) |
下列曲线中离心率为
的是( )
| ||
| 2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
化简:(sin
+cos
)2+2sin2(
-
)得( )
| α |
| 2 |
| α |
| 2 |
| π |
| 4 |
| α |
| 2 |
| A、2+sinα | ||||
B、2+
| ||||
| C、2 | ||||
D、2+
|
 自锐角△ABC的顶点A向边BC引垂线,垂足为D.在AD上任取一点H,直线BH交AC于点E,CH交AB于点F.
自锐角△ABC的顶点A向边BC引垂线,垂足为D.在AD上任取一点H,直线BH交AC于点E,CH交AB于点F.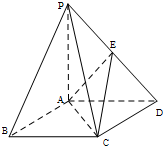 如图,在底面为平行四边形的四棱锥P-ABCD中,AB⊥AC,PA⊥平面ABCD,点E是PD的中点.
如图,在底面为平行四边形的四棱锥P-ABCD中,AB⊥AC,PA⊥平面ABCD,点E是PD的中点.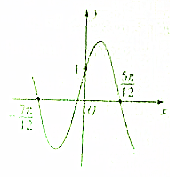 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<