Question

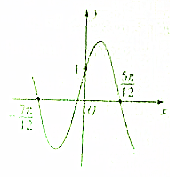已知函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，|φ|＜

π

2

）的部分图象如图所示．
（1）求函数f（x）的解析式；
（2）求函数g（x）=f（

x

2

-

π

12

）•f（

x

2

+

π

12

）的单调递增区间．

Answer 1

考点：正弦函数的图象

专题：三角函数的求值,三角函数的图像与性质

分析：（1）由图观察可得T，即求得ω，由f（

π

6

）=A，可解得φ，由f（x）=Asin（2x+

π

6

）过（0，1），可求得A，从而可求得解析式f（x）=2sin（2x+

π

6

）．
（2）先求解析式得：g（x）=1+2sin（2x-

π

6

），由2kπ-

π

2

≤2x-

π

6

≤2kπ+

π

2

，（k∈Z）即可解得g（x）的单增区间．

解答： 解：（1）由图观察可知：T=（

5π

12

+

7π

12

）=π，
∴ω=

2π

T

=2（∵ω＞0），
∵f（x）=Asin（2x+φ），
∴

T

4

=

π

4

，

5π

12

-

π

4

=

π

6

，
∵f（

π

6

）=A，
∴sin（2×

π

6

+φ）=1，
φ+

π

3

=2kπ+

π

2

，k∈Z，
∴φ=2kπ+

π

6

，k∈Z，
又|φ|＜

π

2

，
∵φ=

π

6

，
∴f（x）=Asin（2x+

π

6

）过（0，1），
∴Asin

π

6

=1，
∴A=2，
∴f（x）=2sin（2x+

π

6

）．
（2）g（x）=f（

x

2

-

π

12

）f（

x

2

+

π

12

）
=2sin[2（

x

2

-

π

12

）+

π

6

]•2sin[2（

x

2

+

π

12

）+

π

6

]
=4sinxsin（x+

π

3

）
=4sinx（

1

2

sinx+

3

2

cosx）
=2sin²x+2

3

sinxcosx
=1-cos2x+

3

sin2x
=1+

3

sin2x-cos2x
=1+2sin（2x-

π

6

），
由2kπ-

π

2

≤2x-

π

6

≤2kπ+

π

2

，（k∈Z），
得：kπ-

π

6

≤x≤kπ+

π

3

，
∴g（x）的单增区间：[kπ-

π

6

，kπ+

π

3

]，（k∈Z）．

点评：本题主要考察了正弦函数的图象和性质，考察了二角和的正弦公式的应用，函数的解析式的求解是解题的关键，属于中档题．