题目内容
化简:(sin
+cos
)2+2sin2(
-
)得( )
| α |
| 2 |
| α |
| 2 |
| π |
| 4 |
| α |
| 2 |
| A、2+sinα | ||||
B、2+
| ||||
| C、2 | ||||
D、2+
|
考点:三角函数中的恒等变换应用
专题:计算题,三角函数的求值
分析:由诱导公式、二倍角公式即可化简求值.
解答:
解::(sin
+cos
)2+2sin2(
-
)=1+sinα+2×
=1+sinα+1-cos(
-α)=2+sinα-sinα=2.
故选:C.
| α |
| 2 |
| α |
| 2 |
| π |
| 4 |
| α |
| 2 |
1-cos[2(
| ||||
| 2 |
| π |
| 2 |
故选:C.
点评:本题主要考察了二倍角公式、诱导公式的应用,属于基础题.

练习册系列答案
相关题目
已知双曲线
-
=1的右焦点为F2(3,0)则该双曲线的焦点到其渐近线的距离等于( )
| x2 |
| 4 |
| y2 |
| b2 |
A、
| ||
B、4
| ||
| C、3 | ||
| D、5 |
 以下给出一个算法的程序框图(如图所示),根据该程序框图回答问题.
以下给出一个算法的程序框图(如图所示),根据该程序框图回答问题.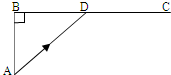 如图,已知海岛A与海岸公路BC的距离为50km,B、C间的距离为100km,从A到C,必须先坐船到BC上某一点D,船速为25km/h,再乘汽车,车速为50km/h.
如图,已知海岛A与海岸公路BC的距离为50km,B、C间的距离为100km,从A到C,必须先坐船到BC上某一点D,船速为25km/h,再乘汽车,车速为50km/h.