题目内容
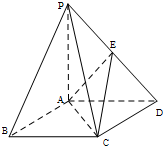 如图,在底面为平行四边形的四棱锥P-ABCD中,AB⊥AC,PA⊥平面ABCD,点E是PD的中点.
如图,在底面为平行四边形的四棱锥P-ABCD中,AB⊥AC,PA⊥平面ABCD,点E是PD的中点.(Ⅰ)求证:PB∥平面AEC;
(Ⅱ)求证:AC⊥PB.
考点:直线与平面平行的判定
专题:空间位置关系与距离
分析:(Ⅰ)欲证PB∥面AEC,根据直线与平面平行的判定定理可知只需证PB与面AEC内一直线平行即可,连接BD交AC于点O,并连接EO,根据中位线可知EO∥PB,PB?面AEC,EO?面AEC满足定理所需条件.
(Ⅱ)欲证AC⊥PB,可先证AC⊥面PAB,根据直线与平面垂直的判定定理可知只需证AC与面PAB内两相交直线垂直,根据PA⊥面ABCD,AC?面ABCD,可得PA⊥AC,又因AB⊥AC,PA∩AC=A,PA?面PAB,AB?面PAB,满足定理所需条件;
(Ⅱ)欲证AC⊥PB,可先证AC⊥面PAB,根据直线与平面垂直的判定定理可知只需证AC与面PAB内两相交直线垂直,根据PA⊥面ABCD,AC?面ABCD,可得PA⊥AC,又因AB⊥AC,PA∩AC=A,PA?面PAB,AB?面PAB,满足定理所需条件;
解答:
证明:(Ⅰ)连接BD交AC于点O,并连接EO,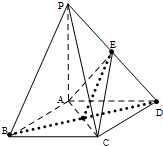
∵四边形ABCD为平行四边形,
∴O为BD的中点又∵E为PD的中点,
∴在△PDB中EO为中位线,EO∥PB,
∵PB?面AEC,EO?面AEC∴PB∥面AEC.
(Ⅱ)∵PA⊥面ABCD,AC?面ABCD,∴PA⊥AC,
又∵AB⊥AC,PA∩AC=A,PA?面PAB,AB?面PAB,
∴AC⊥面PAB,
∴AC⊥PB.

∵四边形ABCD为平行四边形,
∴O为BD的中点又∵E为PD的中点,
∴在△PDB中EO为中位线,EO∥PB,
∵PB?面AEC,EO?面AEC∴PB∥面AEC.
(Ⅱ)∵PA⊥面ABCD,AC?面ABCD,∴PA⊥AC,
又∵AB⊥AC,PA∩AC=A,PA?面PAB,AB?面PAB,
∴AC⊥面PAB,
∴AC⊥PB.
点评:本题考查了空间两直线的位置关系,以及直线与平面平行的判定等有关知识,考查学生空间想象能力,逻辑思维能力,是中档题.

练习册系列答案
相关题目
已知x、y满足条件
则2x+4y的最小值为( )
|
| A、-6 | B、6 | C、-12 | D、12 |
已知O为坐标原点,F为抛物线C:y2=4
x的焦点,P是C上一点,若|PF|=3
,则△OPF的面积为( )
| 3 |
| 3 |
A、2
| ||
B、3
| ||
C、3
| ||
D、6
|
执行如图所示的程序框图,如果输入的N是5,那么输出的P是( )


| A、1 | B、24 | C、120 | D、720 |
 以下给出一个算法的程序框图(如图所示),根据该程序框图回答问题.
以下给出一个算法的程序框图(如图所示),根据该程序框图回答问题.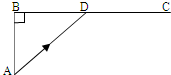 如图,已知海岛A与海岸公路BC的距离为50km,B、C间的距离为100km,从A到C,必须先坐船到BC上某一点D,船速为25km/h,再乘汽车,车速为50km/h.
如图,已知海岛A与海岸公路BC的距离为50km,B、C间的距离为100km,从A到C,必须先坐船到BC上某一点D,船速为25km/h,再乘汽车,车速为50km/h.