题目内容
下列曲线中离心率为
的是( )
| ||
| 2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
考点:双曲线的简单性质
专题:计算题,圆锥曲线的定义、性质与方程
分析:分别求出双曲线的a,b,c,再由离心率公式计算即可得到.
解答:
解:对于A.a=
,b=2,c=
=
,e=
=
;
对于B.a=2,b=
,c=
=
,e=
=
;
对于C.a=2,b=
,c=
=
,e=
=
;
对于D.a=2,b=
,c=
=
,e=
=
.
故离心率为
的是C.
故选C.
| 2 |
| 2+4 |
| 6 |
| c |
| a |
| 3 |
对于B.a=2,b=
| 6 |
| 4+6 |
| 10 |
| c |
| a |
| ||
| 2 |
对于C.a=2,b=
| 2 |
| 4+2 |
| 6 |
| c |
| a |
| ||
| 2 |
对于D.a=2,b=
| 10 |
| 4+10 |
| 14 |
| c |
| a |
| ||
| 2 |
故离心率为
| ||
| 2 |
故选C.
点评:本题考查双曲线的方程和性质,考查离心率的求法,考查运算能力,属于基础题.

练习册系列答案
相关题目
过点(0,1)的直线与抛物线y2=4x仅有一个公共点,则满足条件的直线共有( )条.
| A、0 | B、1 | C、2 | D、3 |
已知O为坐标原点,F为抛物线C:y2=4
x的焦点,P是C上一点,若|PF|=3
,则△OPF的面积为( )
| 3 |
| 3 |
A、2
| ||
B、3
| ||
C、3
| ||
D、6
|
执行如图所示的程序框图,若输入m=7,n=3,则输出的S值为( )


| A、7 | B、42 | C、210 | D、840 |
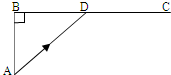 如图,已知海岛A与海岸公路BC的距离为50km,B、C间的距离为100km,从A到C,必须先坐船到BC上某一点D,船速为25km/h,再乘汽车,车速为50km/h.
如图,已知海岛A与海岸公路BC的距离为50km,B、C间的距离为100km,从A到C,必须先坐船到BC上某一点D,船速为25km/h,再乘汽车,车速为50km/h.