题目内容
自锐角△ABC的顶点A向边BC引垂线，垂足为D．在AD上任取一点H，直线BH交AC于点E，CH交AB于点F．证明：∠EDH=∠FDH．（即AD平分ED与DF所成的角）
考点：相似三角形的性质
专题：选作题,立体几何
分析：过A作直线l∥BC，延长DF、DE分别交l于P、Q，证明Rt△ADP≌Rt△ADQ，即可得出结论．
解答：
证明：过A作直线l∥BC，延长DF、DE分别交l于P、Q．
于是有
=
，
=
．…（5分）
又
•
•
=1，
所以
•
•
=1，所以AP=AQ．
所以Rt△ADP≌Rt△ADQ，
从而∠EDH=∠FDH．…（15分）
证明：过A作直线l∥BC，延长DF、DE分别交l于P、Q．于是有
| AP |
| BD |
| AF |
| FB |
| AQ |
| DC |
| AE |
| EC |
又
| AF |
| FB |
| BD |
| DC |
| CE |
| EA |
所以
| AP |
| BD |
| BD |
| DC |
| DC |
| AQ |
所以Rt△ADP≌Rt△ADQ，
从而∠EDH=∠FDH．…（15分）
点评：本题考查三角形全等的证明，考查学生分析解决问题的能力，比较基础．
练习册系列答案
一课四练系列答案
黄冈小状元满分冲刺微测验系列答案
新辅教导学系列答案
阳光同学一线名师全优好卷系列答案
相关题目
若实数x，y满足|x-2|≤y≤a，（a∈（0，+∞）），且z=2x+y的最大值为10，则a的值为（ ）
| A、1 | B、2 | C、3 | D、4 |
过点（0，1）的直线与抛物线y2=4x仅有一个公共点，则满足条件的直线共有（ ）条．
| A、0 | B、1 | C、2 | D、3 |
以下给出一个算法的程序框图（如图所示），根据该程序框图回答问题．已知x、y满足条件
则2x+4y的最小值为（ ）
|
| A、-6 | B、6 | C、-12 | D、12 |
已知O为坐标原点，F为抛物线C：y2=4
x的焦点，P是C上一点，若|PF|=3
，则△OPF的面积为（ ）
| 3 |
| 3 |
A、2
| ||
B、3
| ||
C、3
| ||
D、6
|
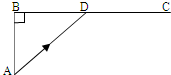如图，已知海岛A与海岸公路BC的距离为50km，B、C间的距离为100km，从A到C，必须先坐船到BC上某一点D，船速为25km/h，再乘汽车，车速为50km/h．