题目内容

棱长为
2
的正四面体的外接球半径为
 
．
考点：球内接多面体
专题：计算题,空间位置关系与距离
分析：正四面体扩展为正方体，它们的外接球是同一个球，正方体的对角线长就是球的直径，求出直径即可求出外接球半径．
解答： 解：正四面体扩展为正方体，它们的外接球是同一个球，
正方体的对角线长就是球的直径，正方体的棱长为：1；对角线长为：
3
，
∴棱长为
2
的正四面体的外接球半径为
3
2
．
故答案为：
3
2
．
点评：本题是基础题，考查正四面体的外接球的半径的求法，本题的突破口在正四面体转化为正方体，外接球是同一个球，考查计算能力，空间想象能力．
练习册系列答案
相关题目
网络公司为了解某地区人群上网情况，随机抽取了100名网民进行调查，其中女性有55名．下面是根据调查结果绘制的日均上网时间的频率分布图（时间单位为：时）：
分组 [0，1） [1，2） [2，3） [3，4） [4，5） [5，6）
频率  0.1 0.18  0.22   0.25 0.2   0.05
将日均上网时间不低于4小时的网民成为“网迷”，已知“网迷”中有10名女性．
（Ⅰ）根据已知条件完成下面2×2列联表，并判断是否有95%的把握认为“网迷”与性别有关？
  非网迷 网迷 合计
男      
女      
合计      
（Ⅱ）将日均上网时间不低于5小时的网民成为“超级网迷”，已知超级网迷中有2名女性，若从“超级网迷”中任意选取2人，求至少有1名女性网民的概率．
附：K2=
n(ad-bc)2
(a+b)(c+d)(a+c)(b+d)

P（K2≥k0）  0.100 0.050  0.010   0.001
 k0  2.706 3.841  6.635  10.828 
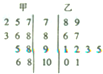某科考试中，从甲、乙两个班级各随机抽取10名同学的成绩进行统计分析，两班成绩的茎叶图如图所示，成绩不小于90分为及格．
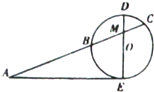（1）分别计算甲、乙两班10名同学成绩的平均数，并估计哪班的成绩更高；
（2）在所抽取的20人中的及格同学中，按分层抽样的方法抽取5人，求甲班恰好抽到一名成绩为100分以上的同学的概率．
如图，AE切圆O于点E，AC交圆O于B，C两点，且与直径DE交于点M，DM=2，CM=3，BM=6，则tanA=
 
．
对于整数a，b，存在唯一一对整数q和r，使得a=bq+r，0≤r＜|b|．特别地，当r=0时，称b能整除a，记作b|a，已知A={1，2，3，…，23}，若B⊆A，card（B）=12（card（B）指集合B中的元素的个数），且存在a，b∈B，b＜a，b|a，则称B为“谐和集”．
（1）若存在q∈A，使得2014=92q+r（0≤r＜92），则r=
 
；
（2）若集合A的任意子集C为“谐和集”，且card（C）=12，m∈C，则m的最大值为
 
．
一个几何体的三视图如图所示，则该几何体的体积为
 
．
执行如图所示的程序框图，若输入n的值为12，则输出的S的值为
 
．
设各项均为正整数的无穷等差数列{an}，满足a54=2014，且存在正整数k，使a1，a54，ak成等比数列，则公差d的所有可能取值之和为
 
．
已知动点P（x，y）满足
x+y-2≥0
x-y≤0
y≤2
，动点Q（x，y）在曲线（x-1）2+y2=1上，则|PQ|的最大值与最小值的和为（　　）
A、
5
+1
B、2
2
+1
C、
5
+
2
2
D、3
2
+1

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网