题目内容
已知F1,F2分别是椭圆C的左右焦点,A是椭圆C短轴的一个顶点,B是直线AF2与椭圆C的另一个交点,若∠F1AF2=60°,△AF1B的面积为40
,则椭圆C的方程为 .
| 3 |
考点:椭圆的简单性质
专题:圆锥曲线的定义、性质与方程
分析:根据题意,设出椭圆的方程,直线AB的方程,两方程联立,求出A、B点的坐标,由∴△AF1B的面积S,求出c的值,从而得椭圆C的方程.
解答:
解:根据题意,设椭圆的方程为
+
=1,
结合题意,画出图形,如图所示 ;
;
∵∠F1AF2=60°,
∴a:b:c=2:
:1;
∴椭圆的方程可化为
+
=1,
∴直线AB的方程为y=-
(x-c),
∴
,
解得
,
;
∴△AF1B的面积S=
|F1F2|•(|y1|+|y2|)=
×2c×(
c+
c)=40
,
解得c=5;
∴椭圆C的方程为
+
=1.
故答案为:
+
=1.
| x2 |
| a2 |
| y2 |
| b2 |
结合题意,画出图形,如图所示
 ;
;∵∠F1AF2=60°,
∴a:b:c=2:
| 3 |
∴椭圆的方程可化为
| x2 |
| 4c2 |
| y2 |
| 3c2 |
∴直线AB的方程为y=-
| 3 |
∴
|
解得
|
|
∴△AF1B的面积S=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
3
| ||
| 5 |
| 3 |
解得c=5;
∴椭圆C的方程为
| x2 |
| 100 |
| y2 |
| 75 |
故答案为:
| x2 |
| 100 |
| y2 |
| 75 |
点评:本题考查了直线与圆锥曲线的应用问题,解题时应根据题意,应用待定系数法,结合直线被圆锥曲线所截得的弦长,求出圆锥曲线的标准方程来,是中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知全集U={1,2,3,4,5,6,7,8,9,10},集合A={2,3,5,9},集合B={4,5,6,7,9},则(∁UA)∩(∁UB)=( )
| A、{5,9} |
| B、{2,3} |
| C、{1,8,10} |
| D、{4,6,7} |
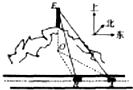 如图,一辆汽车在一条水平的公路上向正西方向行驶,在A处分别测得山顶上铁塔的塔顶E的仰角为θ和山脚点O(点O是点E在公路所在平面上的射影)的方位角是西偏北φ,再行驶akm到达B处,测得山脚点O的方位角是西偏北β.请设计一个方案,用测量的数据和有关公式写出计算OE的步骤.
如图,一辆汽车在一条水平的公路上向正西方向行驶,在A处分别测得山顶上铁塔的塔顶E的仰角为θ和山脚点O(点O是点E在公路所在平面上的射影)的方位角是西偏北φ,再行驶akm到达B处,测得山脚点O的方位角是西偏北β.请设计一个方案,用测量的数据和有关公式写出计算OE的步骤.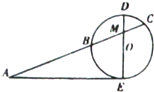 如图,AE切圆O于点E,AC交圆O于B,C两点,且与直径DE交于点M,DM=2,CM=3,BM=6,则tanA=
如图,AE切圆O于点E,AC交圆O于B,C两点,且与直径DE交于点M,DM=2,CM=3,BM=6,则tanA=
