题目内容
已知函数f（x）=log2（3-x），若在[-2，3）上随机取一个实数x0，则使f（x0）≤1成立的概率为 ．
考点：几何概型
专题：概率与统计
分析：不等式log2（3-x0）≤1的解集为：1≤x0≤3，区间的长度为2，根据几何概率模型的意义，用符合题意的区间长度除以所有的区间长度，即得到本题的概率．
解答：
解：由函数f（x）=log2（3-x），f（x0）≤1，
则log2（3-x0）≤1，解得，1≤x0≤3，
得符合题意的区间为[1，3]
而大前提：在区间[-2，3）内随机选一个数
故所求概率等于：P=
=
，
故答案为：
．
则log2（3-x0）≤1，解得，1≤x0≤3，
得符合题意的区间为[1，3]
而大前提：在区间[-2，3）内随机选一个数
故所求概率等于：P=
| 3-1 |
| 3-(-2) |
| 2 |
| 5 |
故答案为：
| 2 |
| 5 |
点评：熟练掌握对数函数的单调性，解出不等式再用几何概率的公式解题，是本小题的关键所在．
练习册系列答案
相关题目
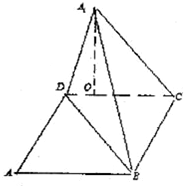如图，矩形ABCD中，AB=10，BC=6，沿对角线BD吧△ABD折起到△A1BD的位置，使A1在平面BCD上的射影O恰好在CD上．
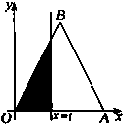如图，△OAB是边长为2的正三角形，记△OAB位于直线x=t（0＜t≤2）左侧的图形的面积为f（t），则
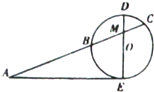如图，AE切圆O于点E，AC交圆O于B，C两点，且与直径DE交于点M，DM=2，CM=3，BM=6，则tanA=