题目内容
求证：对于任意的正整数n，（2+
）n必可表示成
+
的形式，其中s∈N*．
| 3 |
| s |
| s-1 |
考点：二项式定理的应用,数学归纳法
专题：证明题,二项式定理
分析：利用二项式定理，若有(2+
)n=
+
，a，b∈N*，则(2-
)n=
-
，即可得出结论．
| 3 |
| a |
| b |
| 3 |
| a |
| b |
解答：
证明：由二项式定理可知，(2+
)n=
2n(
)0+
2n-1(
)1+
2n-2(
)2+…+
20(
)n，
设(2+
)n=x+
y=
+
，
而若有(2+
)n=
+
，a，b∈N*，
则(2-
)n=
-
，a，b∈N*，
∵(
+
)•(
-
)=(2+
)n•(2-
)n=1，
∴令a=s，s∈N*，则必有b=s-1．
∴(2+
)n必可表示成
+
的形式，其中s∈N*．
| 3 |
| C | 0 n |
| 3 |
| C | 1 n |
| 3 |
| C | 2 n |
| 3 |
| C | n n |
| 3 |
设(2+
| 3 |
| 3 |
| x2 |
| 3y2 |
而若有(2+
| 3 |
| a |
| b |
则(2-
| 3 |
| a |
| b |
∵(
| a |
| b |
| a |
| b |
| 3 |
| 3 |
∴令a=s，s∈N*，则必有b=s-1．
∴(2+
| 3 |
| s |
| s-1 |
点评：本题考查二项式定理的运用，考查学生分析解决问题的能力，正确运用二项式定理是关键．
练习册系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
已知边长为1的正三角形ABC，D是BC的中点，E是AC上一点且AE=2EC．则
•
=（ ）
| AD |
| BE |
A、
| ||
B、-
| ||
| C、0 | ||
| D、4 |
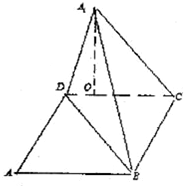如图，矩形ABCD中，AB=10，BC=6，沿对角线BD吧△ABD折起到△A1BD的位置，使A1在平面BCD上的射影O恰好在CD上．
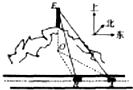如图，一辆汽车在一条水平的公路上向正西方向行驶，在A处分别测得山顶上铁塔的塔顶E的仰角为θ和山脚点O（点O是点E在公路所在平面上的射影）的方位角是西偏北φ，再行驶akm到达B处，测得山脚点O的方位角是西偏北β．请设计一个方案，用测量的数据和有关公式写出计算OE的步骤．