题目内容
在等差数列{an}中，a1=3且a1，a4，a10成等比数列，则（ ）
| A、an=2n+1 |
| B、an=n+2 |
| C、an=2n+1或an=3 |
| D、an=n+2或an=3 |
考点：等差数列的性质
专题：计算题,等差数列与等比数列
分析：利用等差数列{an}中，a1=3且a1，a4，a10成等比数列，建立方程，求出d，即可求出数列的通项．
解答：
解：∵等差数列{an}中，a1=3且a1，a4，a10成等比数列，
∴（3+3d）2=3（3+9d），
∴d=1或d=0，
∴an=n+2或an=3，
故选：D．
∴（3+3d）2=3（3+9d），
∴d=1或d=0，
∴an=n+2或an=3，
故选：D．
点评：本题考查等比数列的性质，考查等差数列的通项，考查学生的计算能力，比较基础．
练习册系列答案
相关题目
函数f（x）=（m2-m-5）xm-1是幂函数，且当x∈（0，+∞）时f（x）是增函数．则实数m=（ ）
| A、3或-2 | B、-2 |
| C、3 | D、-3或2 |
已知集合A={1，2，3，4}，B={a，b，c}，f：A→B为集合A到集合B的一个函数，那么该函数的值域C的不同情况有（ ）
| A、7种 | B、4种 | C、8种 | D、12种 |
已知f：x→x2是集合A到集合B={0，1，4}的一个映射，则集合A中的元素个数最多有（ ）
| A、3个 | B、4个 | C、5个 | D、6个 |
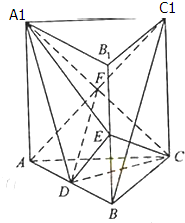如图，三棱柱ABC-A1B1C1中，AA1⊥面ABC，D，E分别是AB，BB1的中点，AA1=AC=CB=4，AB=4