题目内容
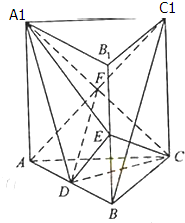 如图,三棱柱ABC-A1B1C1中,AA1⊥面ABC,D,E分别是AB,BB1的中点,AA1=AC=CB=4,AB=4
如图,三棱柱ABC-A1B1C1中,AA1⊥面ABC,D,E分别是AB,BB1的中点,AA1=AC=CB=4,AB=4| 2 |
(Ⅰ)证明:BC1∥平面A1CD;
(Ⅱ) 过点E作一个平面α,使得α∥平面A1CD,求α与直棱柱ABC-A1B1C1的截面面积.
考点:直线与平面平行的判定,棱柱、棱锥、棱台的体积
专题:空间位置关系与距离
分析:(1)连接AC1,交A1C于点F,利用三角形的中位线证明BC1∥DF,即可证明BC1∥平面A1CD;
(2)先把平面α做出来,再求其面积即可.
(2)先把平面α做出来,再求其面积即可.
解答:
(1)证明:连接AC1,交A1C于点F,
则F为AC1中点,
又D是AB中点,连接DF,则BC1∥DF.
因为DF?平面A1CD,BC1?平面AC1D,
所以BC1∥平面A1CD.…(6分)
(2)分别去BD、BC的中点为M、N,
连接MN,EM,EN,
则MN∥DC,EN∥A1D,
∴平面MNE∥平面A1CD,及α为平面MNE,
∵三棱柱ABC-A1B1C1中,AA1⊥面ABC,D,E分别是AB,BB1的中点,AA1=AC=CB=4,AB=4
,
可得:MN=EN=
,ME=
,
可求得:S△MNE=
.
故α与直棱柱ABC-A1B1C1的截面面积为
.
则F为AC1中点,
又D是AB中点,连接DF,则BC1∥DF.
因为DF?平面A1CD,BC1?平面AC1D,
所以BC1∥平面A1CD.…(6分)
(2)分别去BD、BC的中点为M、N,
连接MN,EM,EN,
则MN∥DC,EN∥A1D,
∴平面MNE∥平面A1CD,及α为平面MNE,
∵三棱柱ABC-A1B1C1中,AA1⊥面ABC,D,E分别是AB,BB1的中点,AA1=AC=CB=4,AB=4
| 2 |
可得:MN=EN=
| 2 |
| 6 |
可求得:S△MNE=
| ||
| 2 |
故α与直棱柱ABC-A1B1C1的截面面积为
| ||
| 2 |
点评:本题主要考查线面平行的判定和性质以及截面的性质和面积的求法.

练习册系列答案
相关题目
在等差数列{an}中,a1=3且a1,a4,a10成等比数列,则( )
| A、an=2n+1 |
| B、an=n+2 |
| C、an=2n+1或an=3 |
| D、an=n+2或an=3 |
定义在R上的奇函数f(x),满足f(1)=0,且在(0,+∞)上单调递增,则xf(x)>0的解集为( )
| A、{x|x<-1或x>1} |
| B、{x|0<x<1或-1<x<0} |
| C、{x|0<x<1或x<-1} |
| D、{x|-1<x<0或x>1} |
下列说法错误的是( )
| A、命题“若a=0,则ab=0”的否命题是:“若a≠0,则ab≠0” | ||
| B、如果命题“¬p”与命题“p或q”都是真命题,那么命题q一定是真命题 | ||
| C、若命题p:?x∈R,x2-x+1<0,则¬p:?x∈R,x2-x+1≥0 | ||
D、“sinθ=
|