题目内容
已知函数f(x)=
.
(Ⅰ)写出函数f(x)的导函数,并用定义证明;
(Ⅱ)求函数f(x)图象在点P(1,f(1))处的切线方程.
| 1 |
| x |
(Ⅰ)写出函数f(x)的导函数,并用定义证明;
(Ⅱ)求函数f(x)图象在点P(1,f(1))处的切线方程.
考点:利用导数研究曲线上某点切线方程,利用导数研究函数的单调性
专题:综合题,导数的概念及应用
分析:(Ⅰ)利用导数公式求导数,再用定义证明;
(Ⅱ)求出切线的斜率,切点的坐标,即可求函数f(x)图象在点P(1,f(1))处的切线方程.
(Ⅱ)求出切线的斜率,切点的坐标,即可求函数f(x)图象在点P(1,f(1))处的切线方程.
解答:
解:(Ⅰ)f′(x)=-
,…(1分)
用定义证明如下:
=
=
,…(5分)
让d趋于0,上式趋于-
.…(7分)
(Ⅱ)f(1)=1,故P(1,1).…(8分)
由(Ⅰ)可知,曲线f(x)在点P处的切线斜率为k=f′(1)=-1,…(10分)
所以所求切线方程为y-1=-(x-1)…(12分)
即x+y-2=0.…(13分)
| 1 |
| x2 |
用定义证明如下:
| f(x+d)-f(x) |
| d |
| ||||
| d |
| -1 |
| x(x+d) |
让d趋于0,上式趋于-
| 1 |
| x2 |
(Ⅱ)f(1)=1,故P(1,1).…(8分)
由(Ⅰ)可知,曲线f(x)在点P处的切线斜率为k=f′(1)=-1,…(10分)
所以所求切线方程为y-1=-(x-1)…(12分)
即x+y-2=0.…(13分)
点评:本题主要考查导数的定义、导数的几何意义以及曲线的切线等基础知识.考查运算化简能力、推理论证能力和极限思想.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
cos9°cos36°-sin36°sin9°的值为( )
A、
| ||||
B、
| ||||
C、
| ||||
| D、1 |
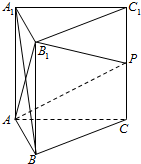 如图,已知点P是正三棱柱ABC-A1B1C1的棱CC1的中点.
如图,已知点P是正三棱柱ABC-A1B1C1的棱CC1的中点.