题目内容
圆（x-3）2+y2=4与圆x2+（y-4）2=16的位置关系为（ ）
| A、内切 | B、外切 | C、相交 | D、相离 |
考点：圆与圆的位置关系及其判定
专题：直线与圆
分析：先求出两个圆的圆心和半径，再根据圆心距大于半径之差而小于半径之和，可得两个圆相交．
解答：
解：这两个圆的圆心分别为（3，0）、（0，4）； 半径分别为2、4．
圆心距为5，大于半径之差而小于半径之和，可得两个圆相交，
故选：C．
圆心距为5，大于半径之差而小于半径之和，可得两个圆相交，
故选：C．
点评：本题主要考查圆的标准方程，两个圆的位置关系的判定方法，属于基础题．
练习册系列答案
名师导航单元期末冲刺100分系列答案
相关题目
回归直线方程的系数a，b的最小二乘法估计中，使函数Q（a，b）最小，Q函数指（ ）
A、
| |||
B、
| |||
| C、（y1-a-bx1）2 | |||
| D、|y1-a-bx1| |
函数f（x）=
ax3+
ax2+2a+1的图象经过四个象限，则实数a的取值范围是（ ）
| 1 |
| 3 |
| 1 |
| 2 |
A、-
| ||||
B、-
| ||||
C、-
| ||||
D、-
|
cos9°cos36°-sin36°sin9°的值为（ ）
A、
| ||||
B、
| ||||
C、
| ||||
| D、1 |
定义“D”：△f（x）=f（x+1）-f（x），△2f（x）=△[△f（x）]，△3f（x）=△[△2f（x）]，…，比如f（x）=x2，则有△f（x）=2x+1，△2f（x）=2，现已知f（x）=x2011，则△2012f（x）=（ ）
| A、1×2×3×…×2011 |
| B、1×2×3×…×2012 |
| C、2012 |
| D、0 |
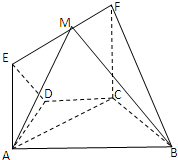如图，在几何体ABCDEF中，AB∥CD，AD=DC=CB=1，∠ABC=60°，四边形ACFE为矩形，平面ACFE⊥平面ABCD，CF=1．