题目内容
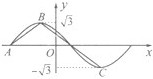如图为函数f（x）=| 3 |
| AB |
| BC |
| AB |
A、
| ||
B、
| ||
C、
| ||
D、
|
考点：函数y=Asin（ωx+φ）的图象变换
专题：三角函数的图像与性质
分析：由图可设A（a，0），函数f（x）=
sin（ωx+φ）的周期为T，则B（a+
，
），C（a+
，-
），易求
=（
，
），
=（
，-2
），利用向量的坐标运算，将已知
•
=|
|2坐标化整理，可求得T=
=12，从而可得ω的值．
| 3 |
| T |
| 4 |
| 3 |
| 3T |
| 4 |
| 3 |
| AB |
| T |
| 4 |
| 3 |
| BC |
| T |
| 2 |
| 3 |
| AB |
| BC |
| AB |
| 2π |
| ω |
解答：
解：设A（a，0），函数f（x）=
sin（ωx+φ）的周期为T，则B（a+
，
），C（a+
，-
），
∴
=（
，
），
=（
，-2
），
∵
•
=|
|2，
∴
•
-2
×
=
+3，
整理得：T2=144，
∴T=
=12，
解得：ω=
．
故选：B．
| 3 |
| T |
| 4 |
| 3 |
| 3T |
| 4 |
| 3 |
∴
| AB |
| T |
| 4 |
| 3 |
| BC |
| T |
| 2 |
| 3 |
∵
| AB |
| BC |
| AB |
∴
| T |
| 4 |
| T |
| 2 |
| 3 |
| 3 |
| T2 |
| 16 |
整理得：T2=144，
∴T=
| 2π |
| ω |
解得：ω=
| π |
| 6 |
故选：B．
点评：本题考查函数y=Asin（ωx+φ）的图象解析式的确定，着重考查向量的数量积的坐标运算及其应用，属于中档题．
练习册系列答案
相关题目
在等比数列{an}中，a1=27，a4=a3a5，则a6=（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
如图所示是根据输入的x计算y值的程序框图，若x依次取数列{| n2+4 |
| n |
| A、4 | B、8 | C、16 | D、32 |
设f（x）是定义在R上的偶函数，?x∈R，都有f（2-x）=f（2+x），且当x∈[0，2]时，f（x）=2x-2，若函数g（x）=f（x）-loga（x+1）（a＞0，a≠1）在区间（-1，9]内恰有三个不同零点，则实数a的取值范围是（ ）
A、（0，
| ||||||||
B、（
| ||||||||
C、（
| ||||||||
D、（
|
在梯形ABCD中，AB∥DC，AD⊥AB，AB=2AD=2DC=4，点N是CD边上一动点，则
•
的最大值为（ ）
| AN |
| AB |
A、4
| ||
| B、8 | ||
C、8
| ||
| D、16 |
已知集合A={1，2，4}，B={y|y=log2x，x∈A}，则A∪B=（ ）
| A、{0，1，2} |
| B、{1，2} |
| C、{0，1，2，4} |
| D、{0，1，4} |