题目内容
15.已知函数f(x)=Asin(ωx+$\frac{π}{6}$),(A>0,ω>0)的最小正周期为T=6π,且f(2π)=2.(Ⅰ)求f(x)的表达式;
(Ⅱ)若g(x)=f(x)+2,求g(x)的单调区间及最大值.
分析 (Ⅰ)根据最小正周期为T=6π,求解ω,根据f(2π)=2.带入可得A的值,可得f(x)的表达式.
(Ⅱ)根据g(x)=f(x)+2可得g(x)的表达式,根据三角函数的图象及性质可得单调区间及最大值.
解答 解:(Ⅰ)函数f(x)=Asin(ωx+$\frac{π}{6}$),
∵最小正周期为T=6π,即$\frac{2π}{ω}=6π$,
可得:ω=$\frac{1}{3}$.
∴f(x)=Asin($\frac{1}{3}$x+$\frac{π}{6}$),
又∵f(2π)=2,A>0、
∴2=Asin($\frac{1}{3}$×2π+$\frac{π}{6}$),
故得A=4.
∴f(x)的表达式为:f(x)=4sin($\frac{1}{3}$x+$\frac{π}{6}$).
(Ⅱ)∵g(x)=f(x)+2,
∴g(x)=4sin($\frac{1}{3}$x+$\frac{π}{6}$)+2
由-$\frac{π}{2}+2kπ≤$$\frac{1}{3}$x+$\frac{π}{6}$≤$\frac{π}{2}+2kπ$,k∈Z
可得:6kπ-2π≤x≤π+6kπ
∴g(x)的单调增区间为[6kπ-2π,π+6kπ],k∈Z
由$\frac{π}{2}+2kπ≤$$\frac{1}{3}$x+$\frac{π}{6}$≤$\frac{3π}{2}+2kπ$,k∈Z
可得:6kπ+π≤x≤4π+6kπ
∴g(x)的单调减区间为[π+6kπ,4π+6kπ],k∈Z.
∵sin($\frac{1}{3}$x+$\frac{π}{6}$)的最大值为1.
∴g(x)=4+2=6,
故得g(x)的最大值为6.
点评 本题给出正弦型三角函数的图象及性质,确定其解析式时关键,属于中档题.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
5.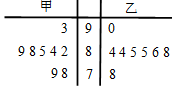 某生产车间的甲、乙两位工人生产同一种零件,这种零件的标准尺寸为85mm,现分别从他们生产的零件中各随机抽取8件检测,其尺寸用茎叶图表示如图(单位:mm),则估计( )
某生产车间的甲、乙两位工人生产同一种零件,这种零件的标准尺寸为85mm,现分别从他们生产的零件中各随机抽取8件检测,其尺寸用茎叶图表示如图(单位:mm),则估计( )
 某生产车间的甲、乙两位工人生产同一种零件,这种零件的标准尺寸为85mm,现分别从他们生产的零件中各随机抽取8件检测,其尺寸用茎叶图表示如图(单位:mm),则估计( )
某生产车间的甲、乙两位工人生产同一种零件,这种零件的标准尺寸为85mm,现分别从他们生产的零件中各随机抽取8件检测,其尺寸用茎叶图表示如图(单位:mm),则估计( )| A. | 甲、乙生产的零件尺寸的中位数相等 | |
| B. | 甲、乙生产的零件质量相当 | |
| C. | 甲生产的零件质量比乙生产的零件质量好 | |
| D. | 乙生产的零件质量比甲生产的零件质量好 |
7.已知F1,F2为双曲线E的左,右焦点,点M在E的渐近线上,△F1F2M为等腰三角形,且顶角为120°,则E的离心率为( )
| A. | $\frac{\sqrt{7}}{2}$ | B. | 2 | C. | $\frac{2\sqrt{3}}{3}$ | D. | $\sqrt{5}$ |
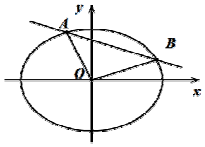 已知椭圆E:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的离心率为$\frac{1}{2}$,且过点$P(1,\frac{3}{2})$,直线l:y=kx+m交椭圆E于不同的两点A,B,设线段AB的中点为M.
已知椭圆E:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的离心率为$\frac{1}{2}$,且过点$P(1,\frac{3}{2})$,直线l:y=kx+m交椭圆E于不同的两点A,B,设线段AB的中点为M.