题目内容

20．函数f（x）=-x2+3x+a，g（x）=2x-x2，若f[g（x）]≥0对x∈[0，1]恒成立，则实数a的取值范围是[-2，+∞）．

分析 先求导判断内函数g（x）的单调性，再参数分离，利用二次函数的单调性可得结论．

解答 解：令t=g（x），x∈[0，1]，则g′（x）=2xln2-2x，
g″（x）=（ln2）2•2x-2＜0，从而g′（x）在[0，1]上单调递减，
设g′（x0）=0，则函数在[0，x0]上单调递增，在[x0，1]上单调递减，
∴t=g（x）在x∈[0，1]上的值域为[1，g（x0）]，其中g（x0）=${2}^{{x}_{0}}$-${x}_{0}^{2}$＜2，
则问题转化为a≥t2-3t在[1，g（x0）]上恒成立，
∵y=t2-3t在（0，$\frac{3}{2}$）上单调递减，在[$\frac{3}{2}$，+∞）上单调递增，
∴y=t2-3t在[1，g（x0）]上的最大值为1-3=-2，
∴a≥-2．
故答案为：[-2，+∞）．

点评 本题考查导数知识的综合运用，考查不等式恒成立问题，注意解题方法的积累，属于难题．

练习册系列答案
相关题目
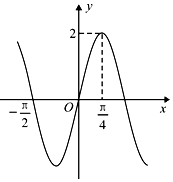10．已知函数f（x）=lnx，曲线y=g（x）与曲线y=f（x）关于直线y=x对称，若存在一条过原点的直线与曲线y=f（x）和曲线y=g（ax）都相切，则实数a的值为$\frac{1}{e^2}$．
11．已知函数f（x）=Asin（ωx）（ω＞0）的图象如图所示．
（Ⅰ）求f（x）的解析式；
（Ⅱ）若$g（x）=f（x）•cos（2x+\frac{π}{6}）$，求g（x）在$[0，\frac{π}{2}]$上的单调递减区间．
8．已知在直角坐标系xOy中，直线l的参数方程为$\left\{\begin{array}{l}{x=t-2}\\{y=\sqrt{3}t}\end{array}\right.$（t为参数），以坐标原点为极点，x轴正半轴为极轴建立极坐标系，曲线C的极坐标方程为ρ2-4ρcosθ+3=0，设点P是曲线C上的一个动点，则P到直线l距离的取值范围是[2$\sqrt{3}$-1，2$\sqrt{3}$+1]．
15．已知函数f（x）=Asin（ωx+$\frac{π}{6}$），（A＞0，ω＞0）的最小正周期为T=6π，且f（2π）=2．
（Ⅰ）求f（x）的表达式；
（Ⅱ）若g（x）=f（x）+2，求g（x）的单调区间及最大值．
5．已知函数f（x）=（x+m）lnx-（m+1+$\frac{1}{e}$）x在x=e处取到极值
（Ⅰ）求m的值
（Ⅱ）当x＞1时，证明f（x）+（2+$\frac{1}{e}$）x＞2x-2
（Ⅲ）如果s，t，r满足|s-r|≤|t-r|，那么称s比t更靠近r，当a≥2且x≥1时，试比较$\frac{e}{x}$和ex-1+a哪个更靠近f（x），并说明理由．
12．已知函数f（x）=$\frac{lnx}{x}$．
（Ⅰ）求函数f（x）的单调区间和最大值；
（Ⅱ）设g（x）=xf（x）+2x，试问：过点（2，5）可作多少条直线与曲线y=g（x）相切？并证明你的结论；
（Ⅲ）若两不等的正数m，n满足mn=nm，函数f（x）的导数为f′（x），证明：f′（$\frac{m+n}{2}$）＜0．
14．已知函数$f（x）=\frac{{{2^x}-a}}{{{2^x}+a}}$是奇函数，其中a∈R，求a的值．
15．已知命题$p：?{x_0}∈R，使x_0^2+{x_0}+1＜0，命题q：?a∈R，若b＞c，则ab＞ac$，给出下列结论：
①命题“p∧q”是真命题
②命题“p∨q”是真命题
③命题“（?p）∨q”是真命题
④命题“（?p）∧（?q）”是真命题
其中正确的是（　　）
A．①③B．①④C．②③D．③④

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网