题目内容
6.已知{an}为等差数列,Sn为其前n项和.若a2=2,S9=9,则a8=0.分析 利用等差数列的通项公式和前n项和公式列出方程组,求出首项和公差,由此能求出a8.
解答 解:{an}为等差数列,Sn为其前n项和.
a2=2,S9=9,
∴$\left\{\begin{array}{l}{{a}_{2}={a}_{1}+d=2}\\{{S}_{9}=9{a}_{1}+\frac{9×8}{2}d=9}\end{array}\right.$,
解得a1=$\frac{7}{3}$,d=-$\frac{1}{3}$
∴a8=a1+7d=$\frac{7}{3}$+7×(-$\frac{1}{3}$)=$\frac{7}{3}$-$\frac{7}{3}$=0.
故答案为:0.
点评 本题考查等差数列的第8项的求法,是基础题,解题时要认真审题,注意等差数列的性质的合理运用.

练习册系列答案
 新编小学单元自测题系列答案
新编小学单元自测题系列答案 字词句段篇系列答案
字词句段篇系列答案
相关题目
16.已知两个随机变量x,y之间的相关关系如表所示:
根据上述数据得到的回归方程为$\widehat{y}$=$\widehat{b}$x+$\widehat{a}$,则大致可以判断( )
| x | -4 | -2 | 1 | 2 | 4 |
| y | -5 | -3 | -1 | -0.5 | 1 |
| A. | $\widehat{a}$>0,$\widehat{b}$>0 | B. | $\widehat{a}$>0,$\widehat{b}$<0 | C. | $\widehat{a}$<0,$\widehat{b}$>0 | D. | $\widehat{a}$<0,$\widehat{b}$<0 |
17.已知命题$p:?n∈N,{2^n}>\sqrt{n}$,则¬p是( )
| A. | $?n∈N,{2^n}≤\sqrt{n}$ | B. | $?n∈N,{2^n}<\sqrt{n}$ | C. | $?n∈N,{2^n}≤\sqrt{n}$ | D. | $?n∈N,{2^n}>\sqrt{n}$ |
18.如果$a={2^{1.2}},b={(\frac{1}{2})^{0.3}},c=2{log_2}\sqrt{3}$,那么( )
| A. | c>b>a | B. | c>a>b | C. | a>b>c | D. | a>c>b |
1.正四面体(四个面都为正三角形)ABCD中,异面直线AB与CD所成的角为( )
| A. | 90° | B. | 60° | C. | 45° | D. | 30° |
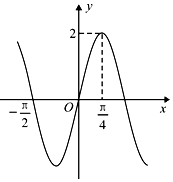 已知函数f(x)=Asin(ωx)(ω>0)的图象如图所示.
已知函数f(x)=Asin(ωx)(ω>0)的图象如图所示.