题目内容
7．已知F1，F2为双曲线E的左，右焦点，点M在E的渐近线上，△F1F2M为等腰三角形，且顶角为120°，则E的离心率为（ ）| A． | $\frac{\sqrt{7}}{2}$ | B． | 2 | C． | $\frac{2\sqrt{3}}{3}$ | D． | $\sqrt{5}$ |
分析 由题意求得M点坐标，代入渐近线方程，求得a与b的关系，利用双曲线的离心率公式即可求得E的离心率．
解答 解：设双曲线方程$\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{{b}^{2}}=1$（a＞0，b＞0），设M在第一象限，
则过M做MD⊥F1F2，
由△F1F2M为等腰三角形，且顶角为120°，则∠MF2D=60°，
丨MF2丨=丨F1F2丨=2c，
∴丨MD丨=$\sqrt{3}$c，丨F2D丨=c，
∴M点坐标为（2c，$\sqrt{3}$c），
由M双曲线的渐近线y=$\frac{b}{a}$x，则$\frac{b}{a}$=$\frac{\sqrt{3}}{2}$，
双曲线的离心率e=$\frac{c}{a}$=$\sqrt{1+\frac{{b}^{2}}{{a}^{2}}}$=$\frac{\sqrt{7}}{2}$，
故选A．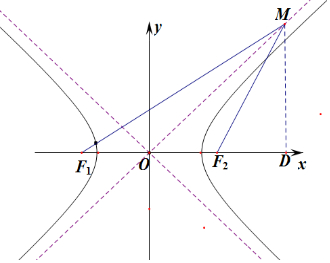
点评 本题考查双曲线的简单几何性质，考查双曲线的渐近线方程，考查计算能力，属于中档题．
练习册系列答案
名校练考卷期末冲刺卷系列答案
相关题目
17．已知命题$p：?n∈N，{2^n}＞\sqrt{n}$，则￢p是（ ）
| A． | $?n∈N，{2^n}≤\sqrt{n}$ | B． | $?n∈N，{2^n}＜\sqrt{n}$ | C． | $?n∈N，{2^n}≤\sqrt{n}$ | D． | $?n∈N，{2^n}＞\sqrt{n}$ |
18．如果$a={2^{1.2}}，b={（\frac{1}{2}）^{0.3}}，c=2{log_2}\sqrt{3}$，那么（ ）
| A． | c＞b＞a | B． | c＞a＞b | C． | a＞b＞c | D． | a＞c＞b |
1．正四面体（四个面都为正三角形）ABCD中，异面直线AB与CD所成的角为（ ）
| A． | 90° | B． | 60° | C． | 45° | D． | 30° |