题目内容
3.已知函数$f(x)=\left\{\begin{array}{l}(x-2a)(a-x),x≤1\\ \sqrt{x}+a-1,x>1.\end{array}\right.$(1)若a=0,x∈[0,4],则f(x)的值域是[-1,1];
(2)若f(x)恰有三个零点,则实数a的取值范围是(-∞,0).
分析 (1)求出f(x)在[-4,4]上的单调性,利用单调性求出最值即可得出值域;
(2)对x讨论,分别求出f(x)的零点,令其零点分别在对应的定义域上即可.
解答 解:(1)a=0时,f(x)=$\left\{\begin{array}{l}{-{x}^{2},x≤1}\\{\sqrt{x}-1,x>1}\end{array}\right.$,
∴f(x)在[0,1]上单调递减,在(1,4]上单调递增,
∵f(0)=0,f(1)=-1,f(4)=1,
∴f(x)在[0,1]上的值域是[-1,0],在(1,4]上的值域是(0,1],
∴f(x)在[0,4]上的值域是[-1,1].
(2)当x≤1时,令f(x)=0得x=2a或x=a,
当x>1时,令f(x)=0得$\sqrt{x}$=1-a,∴x=(1-a)2(1-a>1),
∵f(x)恰好有三个解,
∴$\left\{\begin{array}{l}{2a≤1}\\{a≤1}\\{2a≠a}\\{(1-a)^{2}>1}\\{1-a>1}\end{array}\right.$,解得a<0.
故答案为:[-1,1];(-∞,0).
点评 本题考查了基本初等函数的单调性,函数零点的计算,属于中档题.

练习册系列答案
 百年学典课时学练测系列答案
百年学典课时学练测系列答案 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案
相关题目
18.如果$a={2^{1.2}},b={(\frac{1}{2})^{0.3}},c=2{log_2}\sqrt{3}$,那么( )
| A. | c>b>a | B. | c>a>b | C. | a>b>c | D. | a>c>b |
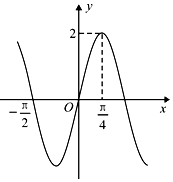 已知函数f(x)=Asin(ωx)(ω>0)的图象如图所示.
已知函数f(x)=Asin(ωx)(ω>0)的图象如图所示.