题目内容
17.设定义在R上的奇函数y=f(x),满足对任意t∈R都有f(t)=f(1-t),且$x∈[0,\frac{1}{2}]$时,f(x)=-x2,则f(2015)的值等于( )| A. | $-\frac{1}{2}$ | B. | $-\frac{1}{4}$ | C. | 0 | D. | $-\frac{1}{8}$ |
分析 根据已知可得函数y=f(x)是周期为2的周期函数,结合$x∈[0,\frac{1}{2}]$时,f(x)=-x2,可得答案.
解答 解:∵函数y=f(x)是定义在R上的奇函数,且f(t)=f(1-t),
∴f(x+2)=f[1-(x+2)]=f(-x-1)=-f(x+1)=-f[1-(x+1)]=-f(-x)=f(x),
即函数y=f(x)是周期为2的周期函数,
故f(2015)=f(1)=-f(0),
又∵$x∈[0,\frac{1}{2}]$时,f(x)=-x2,
∴f(2015)=f(1)=-f(0)=0,
故选:C
点评 本题考查的知识点是函数的奇偶性,函数的对称性,函数的周期性,函数求值,根据已知分析出函数y=f(x)是周期为2的周期函数,是解答的关键.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
5.设a,b∈R,命题“若a>1且b>1,则a+b>2”的逆否命题是( )
| A. | 若a≤1且b≤1,则a+b≤2 | B. | 若a≤1或b≤1,则a+b≤2 | ||
| C. | 若a+b≤2,则a≤1且b≤1 | D. | 若a+b≤2,则a≤1或b≤1 |
2.已知集合U={1,2,3,4},A={1,3},B={1,3,4},则A∪(∁UB)=( )
| A. | {1,3} | B. | {1,2,3} | C. | {1,2,3,4} | D. | {1,3,4} |
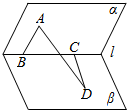 如图,已知B、C是二面角α-l-β棱上两点AB?α,AB⊥l,CD?β,CD⊥l,AB=BC=1,CD=$\sqrt{3}$,AD=2$\sqrt{2}$,则二面角α-l-β的大小是150°.
如图,已知B、C是二面角α-l-β棱上两点AB?α,AB⊥l,CD?β,CD⊥l,AB=BC=1,CD=$\sqrt{3}$,AD=2$\sqrt{2}$,则二面角α-l-β的大小是150°.