题目内容
7.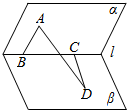 如图,已知B、C是二面角α-l-β棱上两点AB?α,AB⊥l,CD?β,CD⊥l,AB=BC=1,CD=$\sqrt{3}$,AD=2$\sqrt{2}$,则二面角α-l-β的大小是150°.
如图,已知B、C是二面角α-l-β棱上两点AB?α,AB⊥l,CD?β,CD⊥l,AB=BC=1,CD=$\sqrt{3}$,AD=2$\sqrt{2}$,则二面角α-l-β的大小是150°.
分析 将向量 $\overrightarrow{AD}$转化成 $\overrightarrow{AD}$=$\overrightarrow{AB}$+$\overrightarrow{BD}$+$\overrightarrow{DC}$,然后等式两边同时平方表示出向量 $\overrightarrow{AD}$、$\overrightarrow{CD}$的模,再根据向量的数量积求出向量 $\overrightarrow{CD}$与 $\overrightarrow{BA}$的夹角,而两个向量 的夹角大小就是二面角的大小.
解答 解:由条件,知AB⊥l,$\overrightarrow{BC}$•$\overrightarrow{AB}$=0,CD⊥l可得:$\overrightarrow{BC}$•$\overrightarrow{CD}$=0,$\overrightarrow{AD}$=$\overrightarrow{AB}$+$\overrightarrow{BC}$+$\overrightarrow{CD}$,
AB=BC=1,CD=$\sqrt{3}$,AD=2$\sqrt{2}$,
所以$\overrightarrow{AD}$2=$\overrightarrow{AB}$2+$\overrightarrow{BC}$2+$\overrightarrow{CD}$2+2$\overrightarrow{AB}$•$\overrightarrow{BC}$+2$\overrightarrow{BC}$•$\overrightarrow{CD}$+2$\overrightarrow{CD}$•$\overrightarrow{AB}$
=1+1+3+2×1×$\sqrt{3}$cos<$\overrightarrow{AB}$,$\overrightarrow{CD}$>=8
∴cos<$\overrightarrow{AB}$,$\overrightarrow{CD}$>=$\frac{\sqrt{3}}{2}$.
所以<$\overrightarrow{AB}$,$\overrightarrow{CD}$>=30°,<$\overrightarrow{AB}$,$\overrightarrow{CD}$>=150°
所以二面角的大小为150°
故答案为:150°.
点评 本题主要考查了二面角的计算,考查空间想象能力、运算能力和推理论证能力,属于中档题.

| A. | -$\frac{1}{4}$ | B. | -$\frac{7}{4}$ | C. | -$\frac{5}{4}$ | D. | -$\frac{3}{4}$ |
| A. | (0,$\frac{π}{6}$] | B. | (0,$\frac{π}{3}$] | C. | (0,$\frac{π}{2}$] | D. | [$\frac{π}{3}$,$\frac{2π}{3}$] |
| A. | $\frac{1}{27}$ | B. | 2 | C. | -27 | D. | 9 |
| A. | y=-x-1 | B. | y=x+1 | C. | y=x-1 | D. | y=-x+1 |
| A. | $-\frac{1}{2}$ | B. | $-\frac{1}{4}$ | C. | 0 | D. | $-\frac{1}{8}$ |