题目内容
已知平面上两个点集M={(x,y)||x+y+1|≥
,x,y∈R},N={(x,y)||x-a|+|y-1|≤1,x,y∈R}.若M∩N≠∅,则a的取值范围是 .
| 2(x2+y2) |
考点:函数与方程的综合运用,交集及其运算,绝对值不等式的解法
专题:计算题,数形结合
分析:判断集合M的点集,以及集合N的点集,利用函数与方程的特征,求出方程的解,然后判断a的范围即可.
解答:
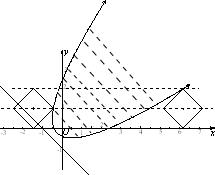 解:由题意知 M 是以原点为焦点、直线 x+y+1=0 为准线的抛物线上及其凹口内侧的点集,N 是以 (a,1)为中心的正方形及其内部的点集(如图).
解:由题意知 M 是以原点为焦点、直线 x+y+1=0 为准线的抛物线上及其凹口内侧的点集,N 是以 (a,1)为中心的正方形及其内部的点集(如图).
考察M∩N=∅时,a的取值范围:
令 y=1,代入方程|x+y+1|≥
,
得 x2-4x-2=0,解出得 x=2±
. 所以,
当 a<2-
-1=1-
时,M∩N=∅. …①
令 y=2,代入方程|x+y+1|≥
,
得x2-6x-1=0,解出得 x=3±
.
所以,当 a>3+
时,M∩N=∅. …②
因此,综合 ①与 ②可知,当 1-
≤a≤3+
,即 a∈[1-
,3+
]时,
M∩N≠∅.
故答案为:[1-
,3+
].
 解:由题意知 M 是以原点为焦点、直线 x+y+1=0 为准线的抛物线上及其凹口内侧的点集,N 是以 (a,1)为中心的正方形及其内部的点集(如图).
解:由题意知 M 是以原点为焦点、直线 x+y+1=0 为准线的抛物线上及其凹口内侧的点集,N 是以 (a,1)为中心的正方形及其内部的点集(如图).考察M∩N=∅时,a的取值范围:
令 y=1,代入方程|x+y+1|≥
| 2(x2+y2) |
得 x2-4x-2=0,解出得 x=2±
| 6 |
当 a<2-
| 6 |
| 6 |
令 y=2,代入方程|x+y+1|≥
| 2(x2+y2) |
得x2-6x-1=0,解出得 x=3±
| 10 |
所以,当 a>3+
| 10 |
因此,综合 ①与 ②可知,当 1-
| 6 |
| 10 |
| 6 |
| 10 |
M∩N≠∅.
故答案为:[1-
| 6 |
| 10 |
点评:本题考查集合的交集的求法,函数的零点以及函数与方程的综合应用,考查计算能力以及转化思想的应用.

练习册系列答案
 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案
相关题目
“1,x,9成等比数列”是“x=3”的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
已知集合A={x|x2-
x-k=0,x∈(-1,1)},若集合A有且仅有一个元素,则实数k的取值范围是( )
| 3 |
| 2 |
A、(-
| ||||||
B、(
| ||||||
C、[-
| ||||||
D、[-
|
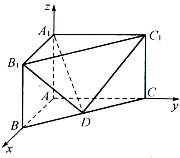 三棱柱ABC-A1B1C1在如图所示的空间直角坐标系中.已知AB=2,AC=4,A1A=3,D是BC的中点.
三棱柱ABC-A1B1C1在如图所示的空间直角坐标系中.已知AB=2,AC=4,A1A=3,D是BC的中点.