题目内容
如图1所示的等边△ABC的边长为2a，CD是AB边上的高，E、F分别是AC、BC边的中点．现将△ABC沿CD折叠成如图2所示的直二面角A-DC-B．
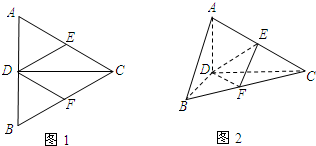
（1）试判断折叠后直线AB与平面DEF的位置关系，并说明理由；
（2）求四面体A-DBC的外接球体积与四棱锥D-ABFE的体积之比．
（1）试判断折叠后直线AB与平面DEF的位置关系，并说明理由；
（2）求四面体A-DBC的外接球体积与四棱锥D-ABFE的体积之比．
考点：与二面角有关的立体几何综合题
专题：空间位置关系与距离
分析：（1）由已知中E、F分别为AC、BC中点，由三角形中位线定理可得EF∥AB，由线面平行的判定定理可得AB∥平面DEF
（2）以DA，DB，DC为棱补成一个长方体，则四面体A-DBC的外接球即为长方体的外接球，进而求出球的体积，和四棱锥D-ABFE的体积，可得答案．
（2）以DA，DB，DC为棱补成一个长方体，则四面体A-DBC的外接球即为长方体的外接球，进而求出球的体积，和四棱锥D-ABFE的体积，可得答案．
解答：
解：（1）如图所示，∵E、F分别为AC、BC的中点，
∴AB∥EF．
∵AB?面DEF，EF?面DEF，
∴AB∥面DEF．
（2）以DA，DB，DC为棱补成一个长方体，则四面体A-DBC的外接球即为长方体的外接球．
设球的半径为R，则a2+a2+3a2=（2R）2，
∴R=
a．
于是球的体积V1=
πR3=
πa3．
又VA-BCD=
•S△BCD•AD=
a3，VE-DFC=
•S△DFC•
AD=
a3，
四棱锥D-ABFE的体积V2=VA-BCD-VE-DFC=
a3．
∴四面体A-DBC的外接球体积与四棱锥D-ABFE的体积之比为
π
∴AB∥EF．
∵AB?面DEF，EF?面DEF，
∴AB∥面DEF．
（2）以DA，DB，DC为棱补成一个长方体，则四面体A-DBC的外接球即为长方体的外接球．
设球的半径为R，则a2+a2+3a2=（2R）2，
∴R=
| ||
| 2 |
于是球的体积V1=
| 4 |
| 3 |
5
| ||
| 6 |
又VA-BCD=
| 1 |
| 3 |
| ||
| 6 |
| 1 |
| 3 |
| 1 |
| 2 |
| ||
| 24 |
四棱锥D-ABFE的体积V2=VA-BCD-VE-DFC=
| ||
| 8 |
∴四面体A-DBC的外接球体积与四棱锥D-ABFE的体积之比为
20
| ||
| 9 |
点评：本题考查的知识点是二面角的平面角及求法，直线与平面平行的判定，点到平面的距离，其中（1）的关键是证得EF∥AB，（2）的关键是计算出四面体A-DBC的外接球体积与四棱锥D-ABFE的体积
练习册系列答案
相关题目
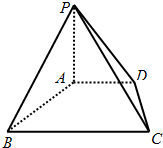已知四棱锥P-ABCD的底面ABCD是直角梯形，AD∥BC，∠ABC=90°，PA⊥平面ABCD，AB=BC=2AD，若平面PCD与平面PAB所成二面角的余弦值为
