Question

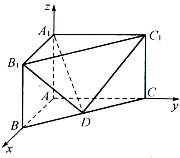三棱柱ABC-A₁B₁C₁在如图所示的空间直角坐标系中．已知AB=2，AC=4，A₁A=3，D是BC的中点．
（1）求直线DB₁与平面A₁C₁D所成角的正弦值；
（2）求二面角B₁-A₁D-C₁的正弦值．

Answer 1

考点：用空间向量求平面间的夹角,直线与平面所成的角

专题：计算题,空间位置关系与距离,空间角

分析：（1）由题中的坐标系，得到A、B、C、D、A₁、B₁、C₁各点的坐标，从而得出

A1D

、

A1C1

的坐标，利用垂直向量数量积为零的方法，建立方程组解出

n

=（3，0，1）是平面A₁C₁D的一个法向量，结合

DB1

=（1，-2，3），
利用空间向量的夹角公式和直线所平面所成角的定义与性质，即可算出直线DB₁与平面A₁C₁D所成角的正弦值；
（2）设平面A₁B₁D的一个法向量为

m

=（a，b，c），由

A1D

、

A1B1

的坐标利用数量积为零建立关于a、b、c的方程组，得到

m

=（0，3，2），结合

n

=（3，0，1）是平面A₁C₁D的一个法向量，利用空间向量的夹角公式算出

n

、

m

夹角的余弦值，再由同角三角函数的关系即可算出二面角B₁-A₁D-C₁的正弦值．

解答： 解：（1）根据题意，可得A（0，0，0），B（2，0，0），C（0，4，0），
D（1，2，0），A₁（0，0，3），B₁（2，0，3），C₁（0，4，3），
∴

A1D

=（1，2，-3），

A1C1

=（0，4，0），
设平面A₁C₁D的一个法向量是

n

=（x，y，z），
可得：

n • A1D =x+2y-3z=0 n • A1C1 =4y=0

，
取z=1，得x=3，y=0，可得

n

=（3，0，1），
设直线DB₁与平面A₁C₁D所成角为α，而

DB1

=（1，-2，3），
∴sinα=|cos＜

n

，

DB1

＞|=

|3×1+0×(-2)+1×3|

10 • 14

=

3 35

35

．
因此，直线DB₁与平面A₁C₁D所成角的正弦值等于

3 35

35

；
（2）设平面A₁B₁D的一个法向量为

m

=（a，b，c），
结合

A1D

=（1，2，-3）、

A1B1

=（2，0，0），可得：

m • A1D =a+2b-3c=0 m • A1B1 =2a=0

，
取b=3，得a=0，c=2，可得

m

=（0，3，2），
设二面角B₁-A₁D-C₁的大小为β，得
|cosβ|=|cos＜

n

，

m

＞|=

| m • n |

| m |•| n |

=

|0×3+3×0+2×1|

13 • 10

=

2

65

∴sinβ=

1-cos 2β

=

3 455

65

，即二面角B₁-A₁D-C₁的正弦值等于

3 455

65

．

点评：本题在指定空间坐标系内求直线与平面所成角和二面角的大小．着重考查了空间向量的夹角公式和利用空间向量研究空间角的知识，属于中档题．同时考查了空间想象能力，逻辑推理能力和运算能力，是一道不错的综合题．