题目内容
已知函数y=
+(2x-1)0+
,求此函数的定义域.
| 1 | ||
1+
|
| 4-x2 |
考点:函数的定义域及其求法
专题:函数的性质及应用,不等式的解法及应用
分析:根据函数式子有意义可得:
解不等式即可得出答案.
|
解答:
解:∵函数y=
+(2x-1)0+
,
∴根据函数式子有意义可得:
,
解不等式得:
,
函数的定义域:[-2,0)∪(0,
)∪(
,1)∪(1,2],
| 1 | ||
1+
|
| 4-x2 |
∴根据函数式子有意义可得:
|
解不等式得:
|
函数的定义域:[-2,0)∪(0,
| 1 |
| 2 |
| 1 |
| 2 |
点评:本题借助求函数的定义域,考查了函数的概念,解不等式等知识,特别容易出错.

练习册系列答案
相关题目
设α是第二象限角,p(x,4)为其终边上的一点,且cosα=
x,则sinα=( )
| 1 |
| 5 |
A、
| ||
B、-
| ||
C、
| ||
D、-
|
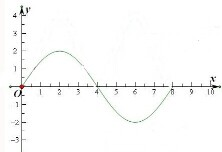 已知函数f(x)=Asinωx(A>0,ω<0)的部分图象如图所示,则函数f(x)是( )
已知函数f(x)=Asinωx(A>0,ω<0)的部分图象如图所示,则函数f(x)是( )| A、周期为8的偶函数 |
| B、周期为8的奇函数 |
| C、周期为8π的偶函数 |
| D、周期为8π的奇函数 |