题目内容
化简:(ex+e-x-4)
+[(ex-e-x)2+4]
.
| 1 |
| 2 |
| 1 |
| 2 |
考点:有理数指数幂的化简求值
专题:函数的性质及应用
分析:由已知得[(ex+e-x)2-4]
+[(ex-e-x)2+4]
=(ex-e-x)+ex+e-x,从而得到x≥0,原式=ex-e-x+ex+e-x=2ex;x<0,原式=-(ex-e-x)+ex+e-x=2e-x-x.
| 1 |
| 2 |
| 1 |
| 2 |
解答:
解:(ex+e-x-4)
+[(ex+e-x)2+4]
=[(ex+e-x)2-4]
+[(ex-e-x)2+4]
=[(e2x+e-2x+2ex•xe-x)-4]
+[(e2x+e-2x-2ex•xe-x)+4]
=(e2x+e-2x-2)
+(e2x+e-2x+2)
=[(ex-e-x)2]
+[(ex+e-x)2]
=(ex-e-x)+ex+e-x,
x≥0,原式=ex-e-x+ex+e-x=2ex;
x<0,原式=-(ex-e-x)+ex+e-x=2e-x-x.
| 1 |
| 2 |
| 1 |
| 2 |
=[(ex+e-x)2-4]
| 1 |
| 2 |
| 1 |
| 2 |
=[(e2x+e-2x+2ex•xe-x)-4]
| 1 |
| 2 |
| 1 |
| 2 |
=(e2x+e-2x-2)
| 1 |
| 2 |
| 1 |
| 2 |
=[(ex-e-x)2]
| 1 |
| 2 |
| 1 |
| 2 |
=(ex-e-x)+ex+e-x,
x≥0,原式=ex-e-x+ex+e-x=2ex;
x<0,原式=-(ex-e-x)+ex+e-x=2e-x-x.
点评:本题考查分数指数幂的化简求值,解题时要认真审题,注意有理数指数幂的运算法则的合理运用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知tanx=5,x的终边落在第一象限,则cosx等于( )
A、
| ||
B、-
| ||
C、
| ||
D、-
|
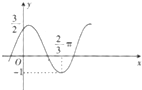 将函数y=Asinωx+b(A,ω,b均为正实数)的图象向左平移
将函数y=Asinωx+b(A,ω,b均为正实数)的图象向左平移| π |
| 12 |
A、y=2sin(x+
| ||||||
B、y=
| ||||||
C、y=
| ||||||
D、y=
|
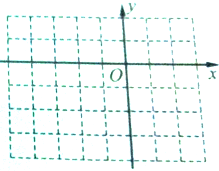 写出下列向量的坐标表示,并在如图所示的正方形网格图中作出下列向量(以O为起点).
写出下列向量的坐标表示,并在如图所示的正方形网格图中作出下列向量(以O为起点). 如图,已知A是△BCD所在平面外一点,M是平面ABC上的一点,试过D、M两点作一平面,使这个平面平行于BC,并说明理由.
如图,已知A是△BCD所在平面外一点,M是平面ABC上的一点,试过D、M两点作一平面,使这个平面平行于BC,并说明理由.