题目内容
已知椭圆C1:
+
=1(a>b>0)的离心率e=
,且经过点(1,
),抛物线C2:x2=2py(p>0)的焦点F与椭圆C1的一个焦点重合.
(1)过F的直线与抛物线C2交于M,N两点,过M,N分别作抛物线C2的切线l1,l2,求直线l1,l2的交点Q的轨迹方程;
(2)从圆O:x2+y2=5上任意一点P作椭圆C1的两条切线,切点为A、B,试问∠APB的大小是否为定值,若是定值,求出这个定值;若不是定值,请说明理由.
| y2 |
| a2 |
| x2 |
| b2 |
| ||
| 3 |
| ||
| 2 |
(1)过F的直线与抛物线C2交于M,N两点,过M,N分别作抛物线C2的切线l1,l2,求直线l1,l2的交点Q的轨迹方程;
(2)从圆O:x2+y2=5上任意一点P作椭圆C1的两条切线,切点为A、B,试问∠APB的大小是否为定值,若是定值,求出这个定值;若不是定值,请说明理由.
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线中的最值与范围问题
分析:(1)利用椭圆与抛物线的标准方程及其性质可得方程.设直线MN的方程为:y=kx+1,与抛物线的方程联立可得根与系数的关系,再利用导数的几何意义可得切线的方程,联立解得即可.
(2)当两条切线的斜率都存在且不为0时,设P(m,n),切线方程为y-n=k(x-m),则m2+n2=5.把切线方程与椭圆方程联立可得△=0,进而得出k1k2+1=0,即可得出.
(2)当两条切线的斜率都存在且不为0时,设P(m,n),切线方程为y-n=k(x-m),则m2+n2=5.把切线方程与椭圆方程联立可得△=0,进而得出k1k2+1=0,即可得出.
解答:
解:(1)∵椭圆C1:
+
=1(a>b>0)的离心率e=
,且经过点(1,
),
∴
,解得c=1,a2=3,b2=2.
∴椭圆C1的方程为
+
=1.
∵抛物线C2:x2=2py(p>0)的焦点F与椭圆C1的一个焦点重合.
∴F(0,1),可得抛物线的方程为x2=4y.
设直线MN的方程为:y=kx+1,M(x1,y1),N(x2,y2).
联立
,化为x2-4kx-4=0.
∴x1+x2=4k,x1x2=-4.
由x2=4y可得y′=
x.
∴切线l1的方程为:y-
=
x1(x-x1),化为y=
x1x-
.
切线l2的方程为:y-
=
x2(x-x2),化为y=
x2x-
.
联立解得x=
=2k,y=
x1x2=-1.
∴直线l1,l2的交点Q的轨迹方程为y=-1.
(2)当两条切线的斜率都存在且不为0时,设P(m,n),
切线方程为y-n=k(x-m),则m2+n2=5.
联立
,
化为(2k2+3)x2+4k(n-km)x+2(n-km)2-6=0,
∴△=0,
化为(2-m2)k2+2mnx+3-n2=0,
∴k1k2=
,
∴k1k2+1=
=0,
可得∠APB=90°.
当条切线的斜率不存在或为0时,即可得出∠APB=90°.
综上可得:从圆O:x2+y2=5上任意一点P作椭圆C1的两条切线,切点为A、B,∠APB=90°为定值.
| y2 |
| a2 |
| x2 |
| b2 |
| ||
| 3 |
| ||
| 2 |
∴
|
∴椭圆C1的方程为
| y2 |
| 3 |
| x2 |
| 2 |
∵抛物线C2:x2=2py(p>0)的焦点F与椭圆C1的一个焦点重合.
∴F(0,1),可得抛物线的方程为x2=4y.
设直线MN的方程为:y=kx+1,M(x1,y1),N(x2,y2).
联立
|
∴x1+x2=4k,x1x2=-4.
由x2=4y可得y′=
| 1 |
| 2 |
∴切线l1的方程为:y-
| ||
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
| x | 2 1 |
切线l2的方程为:y-
| ||
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
| x | 2 2 |
联立解得x=
| x1+x2 |
| 2 |
| 1 |
| 4 |
∴直线l1,l2的交点Q的轨迹方程为y=-1.
(2)当两条切线的斜率都存在且不为0时,设P(m,n),
切线方程为y-n=k(x-m),则m2+n2=5.
联立
|
化为(2k2+3)x2+4k(n-km)x+2(n-km)2-6=0,
∴△=0,
化为(2-m2)k2+2mnx+3-n2=0,
∴k1k2=
| 3-n2 |
| 2-m2 |
∴k1k2+1=
| 5-m2-n2 |
| 2-m2 |
可得∠APB=90°.
当条切线的斜率不存在或为0时,即可得出∠APB=90°.
综上可得:从圆O:x2+y2=5上任意一点P作椭圆C1的两条切线,切点为A、B,∠APB=90°为定值.
点评:本题综合考查了椭圆与抛物线及圆的标准方程及其性质可得方程、直线与椭圆抛物线相交及相切转化为方程联立得到根与系数的关系、及其△与0的关系,考查了导数的几何意义求切线的斜率,考查了推理能力与计算能力,考查了分类讨论的思想方法,属于难题.

练习册系列答案
相关题目
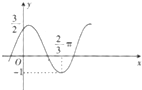 将函数y=Asinωx+b(A,ω,b均为正实数)的图象向左平移
将函数y=Asinωx+b(A,ω,b均为正实数)的图象向左平移| π |
| 12 |
A、y=2sin(x+
| ||||||
B、y=
| ||||||
C、y=
| ||||||
D、y=
|
下列函数中,在其定义域内既是奇函数又是减函数的是( )
A、y=
| ||||||||
B、f(x)=
| ||||||||
C、y=
| ||||||||
| D、y=lg|x| |