题目内容
袋子里有两个不同的红球和两个不同的白球,从中任取两个球,则这两个球颜色相同的概率为 .
考点:古典概型及其概率计算公式
专题:排列组合
分析:从中任取两个球共有红1红2,红1白1,红1白2,红2白1,红2白2,白1白2,共6种取法,其中颜色相同只有2种,根据概率公式计算即可
解答:
解:从中任取两个球共有红1红2,红1白1,红1白2,红2白1,红2白2,白1白2,共6种取法,其中颜色相同只有2种,
故从中任取两个球,则这两个球颜色相同的概率P=
=
;
故答案为:
.
故从中任取两个球,则这两个球颜色相同的概率P=
| 2 |
| 6 |
| 1 |
| 3 |
故答案为:
| 1 |
| 3 |
点评:本题考查了古典概型概率的问题,属于基础题

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
若m,n是不同的直线,α,β是不同的平面,则下列命题中,错误的是( )
| A、若m⊥α,n⊥α,则m∥n |
| B、若m?α,α∥β,则m∥β |
| C、若m∥α,n∥α,则m∥n |
| D、若m∥n,m∥α,n?α,则n∥α |
函数y=cos(2x+
)的图象可由函数y=cos2x的图象( )
| π |
| 4 |
A、向左平移
| ||
B、向右平移
| ||
C、向左平移
| ||
D、向右平移
|
已知命题p:“x>2且是x2>4的充要条件”,命题q:“?x∈R,2x>0”.则下列结论正确的是( )
| A、p∨q为假 |
| B、p∧q为真 |
| C、p∨(¬q)为假 |
| D、p,q均为真 |
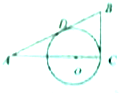 如图,AB和BC分别于圆O相切于点D,C,AC经过圆心O,且BC=2OC=4,则sinA=
如图,AB和BC分别于圆O相切于点D,C,AC经过圆心O,且BC=2OC=4,则sinA=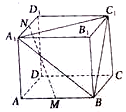 如图所示,长方形ABCD-A1B1C1D1中,M,N分别为AB,A1D1的中点,判断MN与平面A1BC1的位置关系,为什么?
如图所示,长方形ABCD-A1B1C1D1中,M,N分别为AB,A1D1的中点,判断MN与平面A1BC1的位置关系,为什么?