题目内容
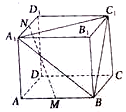如图所示，长方形ABCD-A1B1C1D1中，M，N分别为AB，A1D1的中点，判断MN与平面A1BC1的位置关系，为什么？考点：空间中直线与平面之间的位置关系
专题：空间位置关系与距离
分析：找出C1D1的中点Q，连接NQ，MQ，利用正方体的性质容易得到NQ∥A1C1，MQ∥BC1，得到平面MNQ∥平面A1BC1，MN∥平面A1BC1．
解答：
解：MN∥平面A1BC1．
理由如下：
找出C1D1的中点Q，连接NQ，MQ，如图
因为几何体是正方体，
所以NQ∥A1C1，MQ∥BC1，
所以平面MNQ∥平面A1BC1，
所以MN∥平面A1BC1．
解：MN∥平面A1BC1．理由如下：
找出C1D1的中点Q，连接NQ，MQ，如图
因为几何体是正方体，
所以NQ∥A1C1，MQ∥BC1，
所以平面MNQ∥平面A1BC1，
所以MN∥平面A1BC1．
点评：本题考查了正方体的性质的运用以及线面平行的判定定理的运用．关键是正确运用正方体的性质得到线线平行．
练习册系列答案
相关题目
设f（x）=x+1，那么f（x+1）关于直线x=2对称的曲线的解析式是（ ）
| A、y=x-6 |
| B、y=6+x |
| C、y=6-x |
| D、y=-x-2 |
三个变量y1，y2，y3随着变量x的变化情况如下表：
则与x呈对数型函数、呈指数型函数、呈幂函数型函数变化的变量依次是（ ）
| x | 1 | 3 | 5 | 7 | 9 | 11 |
| y1 | 5 | 135 | 625 | 1715 | 3645 | 6655 |
| y2 | 5 | 29 | 245 | 2189 | 19685 | 177149 |
| y3 | 5 | 6.10 | 6.61 | 6.95 | 7.20 | 7.40 |
| A、y1，y2，y3 |
| B、y2，y1，y3 |
| C、y3，y2，y1 |
| D、y3，y1，y2 |
某舰艇在A处测得遇险渔船在北偏东30°、距离为6
海里的B处，此时得知该渔船正在沿正东方向以每小时6
海里的速度航行，舰艇以每小时18海里的速度去救援，则舰艇追上渔船的最短时间是（ ）
| 3 |
| 3 |
| A、30分钟 | B、40分钟 |
| C、50分钟 | D、60分钟 |
已知a，b∈R，则a=-b是a2+b2≥-2ab的（ ）
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |